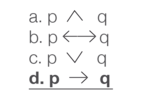Lógica matemática
| (No se muestran 7 ediciones intermedias de otro usuario) | |||
| Línea 8: | Línea 8: | ||
La evaluación es un elemento fundamental en el modelo de la calidad educativa; sin embargo, por sí misma, no mejora los aprendizajes. Es el uso que se haga de | La evaluación es un elemento fundamental en el modelo de la calidad educativa; sin embargo, por sí misma, no mejora los aprendizajes. Es el uso que se haga de | ||
los resultados lo que impacta el alcance de las metas educativas del país. Con el objetivo de facilitar la vinculación de los resultados de la Evaluación Nacional | los resultados lo que impacta el alcance de las metas educativas del país. Con el objetivo de facilitar la vinculación de los resultados de la Evaluación Nacional | ||
| − | de Graduandos con los procesos de | + | de Graduandos con los procesos de enseñanza aprendizaje que se dan en el aula, la Dirección General de Evaluación e Investigación Educativa –DIGEDUCA– del Ministerio de Educación, plantea este material como un instrumento para que docentes y directores puedan reflexionar acerca de los resultados obtenidos en el 2013. Se espera que esta reflexión incida en la tarea que cada docente realiza en cualquiera de las áreas curriculares del Nivel de Educación Media, del Ciclo de |
Educación Diversificada. | Educación Diversificada. | ||
| Línea 116: | Línea 116: | ||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
== <span style="color: #e2007a;">Sugerencias de estrategias de enseñanza-aprendizaje</span> == | == <span style="color: #e2007a;">Sugerencias de estrategias de enseñanza-aprendizaje</span> == | ||
| − | 1. Buscar ejemplos y contraejemplos. Es necesario que el docente estimule a los estudiantes para que trabajen un razonamiento deductivo y que sean ellos quienes generen ejemplos y | + | 1. Buscar ejemplos y contraejemplos. Es necesario que el docente estimule a los estudiantes para que trabajen un razonamiento deductivo y que sean ellos quienes generen ejemplos y contraejemplos que sirvan como demostraciones matemáticas. |
{| style="background:#e2007a;border:1px solid #e2007a;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#e2007a;border:1px solid #e2007a;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 123: | Línea 123: | ||
(Monroy y González, 2009). | (Monroy y González, 2009). | ||
|} | |} | ||
| − | 2. Trabajar en grupos la generación de | + | 2. Trabajar en grupos la generación de proposiciones, discutir cuáles son proposiciones y cuáles no, recordando que pueden ser afirmaciones verdaderas o falsas. Practicar el uso de conec-tores lógicos, considerando no solo la notación sino la lectura de las proposiciones compuestas. Cuando los estudiantes dominen estos conocimientos se puede profundizar en el análisis de las tablas de verdad, considerando la verdad o falsedad de las proposiciones. |
| − | 3. Favorecer la valoración de la argumentación | + | |
| + | 3. Favorecer la valoración de la argumentación lógica al trabajar grupos de debate. Si bien al inicio es posible que a los estudiantes se les dificulte hacer las declaraciones, ha de favorecerse su participación señalando los criterios de rigor lógico. El debate inicia con una proposición elegida por un estudiante (por ejemplo: “Todos los escritores son inteligentes”), el grupo señala si es cierta o falsa. Los estudiantes que consideren la proposición como verdadera, deben demostrarlo argumentando más proposiciones relacionadas o indicando las condiciones bajo las cuales la proposición es verdadera. De igual manera quienes quieran probar la falsedad de la proposición deberán argumentarlo (en el ejemplo dado, algún estudiante podría expresar “no todas las obras escritas reflejan criterio, entonces no todos los escritores son inteligentes”). Los estudiantes deben evaluar todas las proposiciones por su valor lógico, tanto la inicial como las que se deriven de ella, pueden ir anotando las proposiciones de forma simbólica y es válido que se ayuden entre ellos para plantear mejor sus afirmaciones. | ||
== <span style="color: #e2007a;">Referencias</span> == | == <span style="color: #e2007a;">Referencias</span> == | ||
<references /> | <references /> | ||
| − | * DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras. | + | * DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). [[Tabla de contenidos del CNB - Bachillerato en Ciencias y Letras|''Curriculum Nacional Base: Bachillerato en Ciencias y Letras'']]. Guatemala: Ministerio de Educación. |
| − | + | * DIGECUR – Dirección General de Currículo–. (2013a). [[Tabla de Contenidos del CNB - Bachillerato en Ciencias y Letras con Orientación en Educación de Productividad y Desarrollo|''Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo'']]. Guatemala: Ministerio de Educación. | |
| − | * DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación. | + | * DIGECUR – Dirección General de Currículo–. (2013b). [[Tabla de Contenidos del CNB - Bachillerato en Ciencias y Letras con Orientación en Finanzas y Administración|''Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración'']]. Guatemala: Ministerio de Educación. |
| − | * DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación. | + | * González, F. (2005). ''Apuntes de lógica matemática''. Departamento de Matemáticas – Universidad de Cádiz. Obtenido desde http://www2.uca.es/dept/matematicas/Docencia/ESI/1710040/Apuntes/Leccion1.pdf |
| − | * González, F. (2005). Apuntes de lógica matemática. Departamento de Matemáticas – Universidad de Cádiz. Obtenido desde http://www2.uca.es/dept/matematicas/Docencia/ESI/1710040/Apuntes/Leccion1.pdf | + | * López, A. (2009). ''Matemáticas discretas: Lógica matemática''. Obtenido desde http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r44828.PDF |
| − | * López, A. (2009). Matemáticas discretas: Lógica matemática. Obtenido desde http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r44828.PDF | + | * Monroy, A. y González, M. (2009). ''La implicación lógica en el proceso de demostración matemática: estudio de un caso''. Investigación didáctica, 28(2), 73-84. Obtenido desde http://ddd.uab.es/pub/edlc/02124521v28n1/02124521v28n1p73.pdf |
| − | * Monroy, A. y González, M. (2009). La implicación lógica en el proceso de demostración matemática: estudio de un caso. Investigación didáctica, 28(2), 73-84. Obtenido desde http://ddd.uab.es/pub/edlc/02124521v28n1/02124521v28n1p73.pdf | + | * USAID –United States Agency for International Development–. (2009). ''Competencias básicas para la vida''. Guatemala. |
| − | * USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala | + | * Vicente, S., Dooren, W. y Verschaffel, L. 2008. "Utilizar las matemáticas para resolver problemas reales". ''Cultura y Educación'', 20 (4): 391-406. |
| − | * Vicente, S., Dooren, W. y Verschaffel, L. 2008. Utilizar las matemáticas para resolver problemas reales. Cultura y Educación, 20 (4): 391-406. | + | |
| + | [[Category:Matemáticas]] [[Category:Bachillerato]] [[Categoría:Resultados de las evaluaciones]] | ||
Revisión actual del 23:08 8 may 2015
Lógica matemática
Presentación[editar | editar código]
La evaluación es un elemento fundamental en el modelo de la calidad educativa; sin embargo, por sí misma, no mejora los aprendizajes. Es el uso que se haga de los resultados lo que impacta el alcance de las metas educativas del país. Con el objetivo de facilitar la vinculación de los resultados de la Evaluación Nacional de Graduandos con los procesos de enseñanza aprendizaje que se dan en el aula, la Dirección General de Evaluación e Investigación Educativa –DIGEDUCA– del Ministerio de Educación, plantea este material como un instrumento para que docentes y directores puedan reflexionar acerca de los resultados obtenidos en el 2013. Se espera que esta reflexión incida en la tarea que cada docente realiza en cualquiera de las áreas curriculares del Nivel de Educación Media, del Ciclo de Educación Diversificada.
Evaluación de Graduandos[editar | editar código]
Anualmente todos los estudiantes que cursan el último año del ciclo diversificado participan en la Evaluación Nacional de Graduandos. El objetivo del proceso es determinar el nivel de los aprendizajes alcanzados por los alumnos al finalizar su paso por el sistema educativo. Para medir las habilidades desarrolladas, se evalúan contenidos declarativos y procedimentales en el contexto de competencias básicas para la vida.
El área curricular de Matemáticas se incluye en la Evaluación Nacional de Graduandos ya que promueve el desarrollo de los procesos cognitivos necesarios para la comprensión cuantitativa de la realidad. Dentro de esta área se consolidan destrezas relacionadas con análisis, razonamiento y comunicación pertinente y eficaz de ideas, a partir del planteamiento, resolución e interpretación de problemas matemáticos (DIGECADE, 2010; DIGECUR, 2013a; DIGECUR, 2013b). Está vinculada directamente con la competencia básica 3: el uso del pensamiento lógico-matemático para la resolución de problemas de la vida cotidiana.
|
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participen activamente como miembros de la sociedad. Cfr. USAID, 2009, p. 5. |
Las pruebas de Matemáticas evalúan contenidos de sistemas numéricos, aritmética, geometría, trigonometría, álgebra, lógica matemática y estadística. En este documento se analizan, desde los procesos cognitivos, errores comunes que los estudiantes evaluados en el 2013 cometieron al resolver ítems de proposiciones complejas.
¿Cómo usar este documento?[editar | editar código]
Lea la teoría que sustenta y justifica el contenido evaluado. |
Analice el ítem clonado y su descripción. |
A través del análisis del error, identifique posibles debilidades de los estudiantes. |
Decida estrategias a implementar para contribuir al desarrollo de la competencia matemática. |
|
Resultados El porcentaje de respuestas correctas en lógica matemática fue de 24%. Esto quiere decir que si la prueba incluía 5 ítems que evaluaban este contenido, los estudiantes resolvieron correctamente 1.** *El número de ítems varía en las distintas formas de la prueba. |
Lógica matemática[editar | editar código]
Entre otros contenidos específicos se evalúa la lógica de enunciados o proposiciones. En lógica matemática, los literales p, q, r,… denotan variables que pueden reemplazarse por proposiciones. Una proposición es una afirmación en forma de frase que tiene sentido pleno, es decir, puede ser verdadera o falsa pero no ambas cosas a la vez (González, 2005). Por ejemplo:
| Proposiciones | No son proposiciones |
|---|---|
| “6 + 3 = 9” | “¿Te gusta?” |
| “8 es un número impar” | “¡Qué susto!” |
| “La luna brilla todo el día” | “¿Lloverá mañana?” |
| “Carlos Samayoa Chinchilla
escribió ‘Chapines de ayer’ ” |
“¡Levántate ya!” |
Las proposiciones p y q son proposiciones simples que se combinan mediante algún conectivo lógico para formar proposiciones compuestas. Algunas de las conexiones entre proposiciones son:
Análisis del ítem[editar | editar código]
Resolver correctamente este ítem evidencia que el estudiante identifica una situación problema y sus componentes, diseña un plan de acción para abordarlo y aplica correctamente operaciones básicas para resolver la pregunta.
|
Considere la proposición compuesta: Carlos es padre de Juan e Imelda (p), entonces Juan e Imelda son hermanos (q). ¿Cuál de las siguientes expresiones representa la proposición en forma simbólica? |
| Competencia básica 3: Pensamiento lógico-matemático | |
| Dimensión clave | Desarrollo de habilidades de pensamiento lógico. |
| Componente | Modelos matemáticos: formulación de modelos matemáticos diversos como tablas de verdad, relaciones y simulación por computadora. |
| Indicador de logro | Representa información por medio de proposiciones compuestas y tablas de verdad. |
| Contenido evaluado | Utilización de conectivos lógicos |
| Demanda cognitiva | Comprensión |
| Respuesta correcta | Opción d |
Análisis del error[editar | editar código]
| El ítem plantea una proposición compuesta condicional. El estudiante debe identificar el conectivo lógico que le permite representar los enunciados en forma
simbólica. Los estudiantes no fueron capaces de identificar el conectivo lógico condicional “→ ” para expresar simbólicamente la proposición compuesta. Quienes seleccionaron la opción a, confundieron la proposición condicional con una conjunción p^q que en este caso se leería como “Carlos es padre de Juan e Imelda y Juan e Imelda son hermanos”. Si eligieron la opción b, los estudiantes definieron erróneamente la expresión como una proposición bicondicional p↔q que en este caso se leería como “Carlos es padre de Juan e Imelda si y solo si Juan e Imelda son hermanos”. |
Los estudiantes que definieron la opción c como su respuesta, consideraron la proposición como una disyunción pvq que en este caso se leería como “Carlos es padre de Juan e Imelda o Juan e Imelda son hermanos”. Cabe recordar que la lógica se centra en las relaciones entre los enunciados y no en el contenido de un enunciado en particular. De manera que se consideran aquellas expresiones cuyo contenido puede ser evaluado como falso o verdadero. Este tipo de conocimiento matemático permite profundizar en el razonamiento deductivo (López, 2009).
Sugerencias de estrategias de enseñanza-aprendizaje[editar | editar código]
1. Buscar ejemplos y contraejemplos. Es necesario que el docente estimule a los estudiantes para que trabajen un razonamiento deductivo y que sean ellos quienes generen ejemplos y contraejemplos que sirvan como demostraciones matemáticas.
|
“La falta de habilidad para formular postulados, el poco entendimiento intuitivo de los conceptos involucrados [...], imágenes inadecuadas de los conceptos y ausencia de entrenamiento para utilizar sus propios ejemplos”, son fuentes de dificultad para los estudiantes en el desarrollo del pensamiento deductivo implicado en la lógica. (Monroy y González, 2009). |
2. Trabajar en grupos la generación de proposiciones, discutir cuáles son proposiciones y cuáles no, recordando que pueden ser afirmaciones verdaderas o falsas. Practicar el uso de conec-tores lógicos, considerando no solo la notación sino la lectura de las proposiciones compuestas. Cuando los estudiantes dominen estos conocimientos se puede profundizar en el análisis de las tablas de verdad, considerando la verdad o falsedad de las proposiciones.
3. Favorecer la valoración de la argumentación lógica al trabajar grupos de debate. Si bien al inicio es posible que a los estudiantes se les dificulte hacer las declaraciones, ha de favorecerse su participación señalando los criterios de rigor lógico. El debate inicia con una proposición elegida por un estudiante (por ejemplo: “Todos los escritores son inteligentes”), el grupo señala si es cierta o falsa. Los estudiantes que consideren la proposición como verdadera, deben demostrarlo argumentando más proposiciones relacionadas o indicando las condiciones bajo las cuales la proposición es verdadera. De igual manera quienes quieran probar la falsedad de la proposición deberán argumentarlo (en el ejemplo dado, algún estudiante podría expresar “no todas las obras escritas reflejan criterio, entonces no todos los escritores son inteligentes”). Los estudiantes deben evaluar todas las proposiciones por su valor lógico, tanto la inicial como las que se deriven de ella, pueden ir anotando las proposiciones de forma simbólica y es válido que se ayuden entre ellos para plantear mejor sus afirmaciones.
Referencias[editar | editar código]
- DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras. Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación.
- González, F. (2005). Apuntes de lógica matemática. Departamento de Matemáticas – Universidad de Cádiz. Obtenido desde http://www2.uca.es/dept/matematicas/Docencia/ESI/1710040/Apuntes/Leccion1.pdf
- López, A. (2009). Matemáticas discretas: Lógica matemática. Obtenido desde http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r44828.PDF
- Monroy, A. y González, M. (2009). La implicación lógica en el proceso de demostración matemática: estudio de un caso. Investigación didáctica, 28(2), 73-84. Obtenido desde http://ddd.uab.es/pub/edlc/02124521v28n1/02124521v28n1p73.pdf
- USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala.
- Vicente, S., Dooren, W. y Verschaffel, L. 2008. "Utilizar las matemáticas para resolver problemas reales". Cultura y Educación, 20 (4): 391-406.
Indicadores de éxito de un plan escrito en forma específica.
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participaen activamente como miembros de la sociedad.
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Combinación de dos o más palabras usadas con valor comunicativo. La frase puede ser parte de una oración o usarse de manera independiente.
Capacidad o destreza para hacer algo bien o con facilidad.
Conjunto de modos de vida y costumbres, conocimientos y grado de desarrollo artístico, científico, industrial, en una época, grupo social, etc. (DLE). El sistema de creencias, valores, costumbres, conductas y artefactos que los miembros de una sociedad utilizan para enfrentar al mundo y a los demás, y que se transmiten de generación en generación a través del aprendizaje. En este sentido la cultura es fundamental en todo idioma y solo puede aprenderse por medio de la transmisión.