Patrones y relaciones: competencias para la vida
| Línea 406: | Línea 406: | ||
=== Habilidades para el aprendizaje de patrones y relaciones === | === Habilidades para el aprendizaje de patrones y relaciones === | ||
<div style="background-color:#ff2b7f; border-radius:10px; padding:4px; margin:1% auto 3% auto; width:45%; float:right; color:white; clear:both;"> | <div style="background-color:#ff2b7f; border-radius:10px; padding:4px; margin:1% auto 3% auto; width:45%; float:right; color:white; clear:both;"> | ||
| − | '''Comparar:''' Es fijar la atención en dos o más cosas para encontrar parecidos y apreciar diferencias entre ellas | + | '''Comparar:''' Es fijar la atención en dos o más cosas para encontrar parecidos y apreciar diferencias entre ellas <ref>name="Comparar">http://es.thefreedictionary.com/comparar</ref>[[Archivo:Icono ABC transparente.png|right|75px]] |
</div> | </div> | ||
| Línea 414: | Línea 414: | ||
<div style="border:solid 3px; border-color:#ff2b7f; border-radius:10px; padding:4px; margin:2% auto 3% auto; width:65%; clear:right;"> | <div style="border:solid 3px; border-color:#ff2b7f; border-radius:10px; padding:4px; margin:2% auto 3% auto; width:65%; clear:right;"> | ||
| − | [[Archivo:Cuadernillo4 Mate Sexto (17).png|center| | + | [[Archivo:Cuadernillo4 Mate Sexto (17).png|center|550px]] |
</div> | </div> | ||
| Línea 422: | Línea 422: | ||
</div> | </div> | ||
| − | :* Analizar y buscar regularidades La habilidad cognitiva de análisis es necesaria para interpretar y explicar patrones. El estudiante necesita estar expuesto al análisis de patrones, los cuales puede observar en la naturaleza, el entorno sociocultural y también los que le proporcione el docente dentro del aula. | + | :* Analizar y buscar regularidades La habilidad cognitiva de análisis es necesaria para interpretar y explicar patrones. El estudiante necesita estar expuesto al análisis de patrones, los cuales puede observar en la naturaleza, el entorno sociocultural y también los que le proporcione el docente dentro del aula. |
=== Aprender de lo más fácil a lo más difícil === | === Aprender de lo más fácil a lo más difícil === | ||
Revisión del 04:36 26 oct 2016
Las Matemáticas es una de las áreas fundamentales del currículo nacional, porque por medio de ellas se “desarrolla en los alumnos (…), habilidades destrezas y hábitos mentales como: destrezas de cálculo, estimación, observación, representación, argumentación, investigación, comunicación, demostración y autoaprendizaje.”[1]
El aprendizaje de las formas, patrones y relaciones ayuda a los estudiantes a construir elementos geométricos y a aplicar sus propiedades en la resolución de problemas. También ayuda a desarrollar la capacidad de identificar, observar y analizar patrones, tanto en situaciones matemáticas como en actividades de la vida cotidiana.
El componente de Formas, patrones y relaciones, provee al estudiante:
Álgebra:[2] Parte de las matemáticas en la que las operaciones aritméticas se generalizan usando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita.
Circundante: Que rodea algo.- Del lenguaje de la geometría y de las destrezas para distinguir las diversas formas para desarrollar el “sentido espacial y aprender a ver el mundo a través de los ojos de la geometría para construir, dibujar, medir, visualizar, comparar, describir y transformar las cosas”.[3]
- Los patrones y las relaciones permiten identificar cómo estos se manifiestan en la naturaleza y el mundo circundante, así como familiarizarse con el razonamiento y lenguaje algebraico.
- También hacen posible identificar la relación causa efecto en patrones presentes en el entorno natural, social o cultural.[4]
| Las matemáticas, es concebida como la ciencia de los patrones y el orden, ya que es difícil encontrar un área de las matemáticas en la que formalizar y generalizar no sea central.[5] |
¿Qué es un patrón?[editar | editar código]
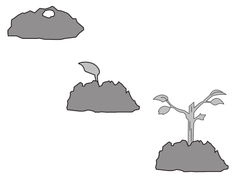
Un patrón es una sucesión de signos orales, gestuales, gráficos, numéricos, entre otros, que se construyen siguiendo una regla, ya sea de repetición o de recurrencia.[6] Los patrones se observan en la vida real y pueden responder a un modelo matemático.
1º. Enterrar la semilla en tierra húmeda.
2º. La semilla absorbe el agua y empieza a respirar.
3º. La semilla al absorber el agua, empieza a respirar y a crecer.
4º. Para seguir creciendo necesita de raíces y estas empiezan a salir.
5º. Con las raíces se puede alimentar mejor y brotan las hojas y los tallos.
El reconocimiento de los patrones existentes, facilita a los estudiantes descubrir argumentos de causa-efecto, presentes en la naturaleza. Por ejemplo:
¿Qué pasa si la semilla se siembra en tierra seca?
¿Por qué los agricultores esperan las primeras lluvias del invierno para empezar a sembrar?
Están formados por sucesión de números y operaciones escritos en un orden definido. Por ejemplo: La secuencia de este patrón está formada por números enteros y decimales.
También son patrones numéricos las coordenadas de un plano cartesiano. Por ejemplo:
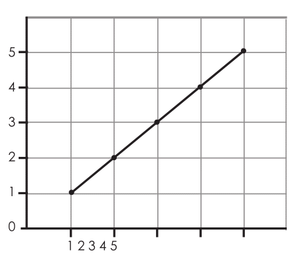 .
.
Los patrones más fáciles de identificar son los que muestran el entorno cultural y natural. La formación de patrones geométricos se considera una estrategia importante para el desarrollo de la creatividad.
Friso: Faja más o menos ancha con la que se decora la parte baja de las paredes. También puede colocarse en la parte alta de un edificio, a modo de coronamiento.
Son patrones geométricos los elementos decorativos de los vestuarios mayas, así como los accesorios: chachales y otros.
También se pueden observar en los elementos decorativos de las casas, ventanas y puertas de las ciudades del país.
| Los patrones decorativos o frisos, además de su valor desde el punto de vista matemático, son una muestra de la aplicación de las matemáticas en el campo del arte.[8] |
Construcción de patrones[9][editar | editar código]
En sexto grado de primaria, los estudiantes aprenderán a identificar la estructura de un patrón y establecer generalizaciones.
Si durante los grados de escolaridad anteriores, el estudiante ha ejercitado las habilidades necesarias para identificar patrones, en el último grado de la primaria, debe ser capaz, además de reconocer los patrones, “construir series numéricas aplicando distintos patrones.”[10]
La construcción de patrones en este grado supone mayor grado de complejidad que en tercero primaria. El estudiante debe ser capaz de identificar y sustituir el número faltante en una serie numérica combinando dos o tres operaciones básicas. De igual manera debe estar preparado para identificar qué tipo de relaciones se dan en las sucesiones dadas.
La estructura básica o núcleo de un patrón, puede ser de repetición o de recurrencia.
Repetición
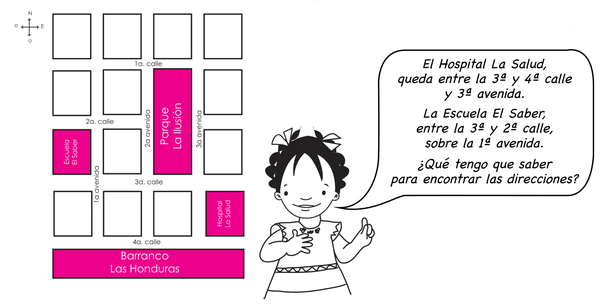
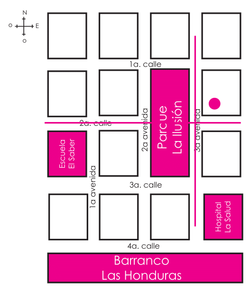
Cuando los patrones se construyen siguiendo una regla de repetición, los elementos de que están compuestos se presentan de forma periódica. Existen y pueden crearse patrones de repetición teniendo en cuenta su estructura de base o núcleo. Un ejemplo de ellos, es el sistema de numeración de las calles y avenidas de la ciudad capital.
¿Qué patrón numérico sigue la dirección de mi casa?
Dirección: 2ª calle 3-20, zona 1.
Si dice 2ª calle, debo buscar en el mapa, la calle identificada con ese número.
El número 3 me indica que debo buscar sobre la 3ª avenida y el número 20, me indica a cuantos metros de distancia de la 3ª avenida está mi casa.
Para encontrar las direcciones, debo conocer qué patrón siguen.
Recurrencia[editar | editar código]
Recurrencia:Cualidad de recurrente.
Sucesión: Conjunto ordenado de términos, que cumplen una ley determinada.
Nascencia: Acción y efecto de nacer.Cuando los patrones se construyen siguiendo una regla de recurrencia, la regularidad con que se presentan los elementos cambia y de ellos tiene que inferirse su ley de formación.
[Archivo:Cuadernillo4 Mate Sexto (13).png|left|100px]] Leyendo una revista de agricultura, me encontré que para conseguir buenas cosechas de maíz, es importante regar los cultivos correctamente.
La necesidad de agua es diferente según van creciendo las plantas. Encontré la siguiente información.
| Semana | Estado de crecimiento | Metros cúbicos (m3) necesarios |
|---|---|---|
| 1ª | Siembra | 42 |
| 2ª | Nascencia | 42 |
| 3ª | Desarrollo primario | 52 |
| 5ª | Crecimiento | 120 |
| 8ª | Floración | 185 |
| 9ª | Polinización | 190 |
| 11ª | Fecundación | 200 |
| 12ª | Crecimiento y maduración de la mazorca | |
| 14ª | Semana |
Cuando terminé de leer, se me presentaron algunas dudas:
- El maíz, ¿necesita la misma cantidad de agua cuando se siembra y cuando nace?
- ¿Cuándo más necesita? ¿Qué datos me responden esa pregunta?
- ¿Cuál es el momento en que el cultivo de maíz necesita más agua?
- ¿Cuántos metros cúbicos más necesita el cultivo durante el periodo de fecundación, que durante el periodo de siembra?
- Durante el periodo de crecimiento y maduración hasta la 15ª semana, los cultivos necesitan la misma cantidad de agua. ¿Cuántos metros cúbicos de agua necesitan, si se les debe dar 2 m3 menos que durante el periodo de fecundación?
Y… ¿las relaciones?[editar | editar código]
Se entiende por relación la forma en que se comporta un elemento con relación a otro del mismo patrón. Al analizar la estructura del patrón y el orden de sus elementos, es posible determinar la relación existente entre ellos. Por ejemplo:
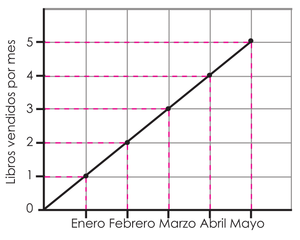
Relación de uno a uno La gráfica muestra relación de uno a uno, porque cada mes se relaciona con una determinada cantidad de libros vendidos.
Relación de dependencia Si se proporciona a los cultivos de maíz la cantidad necesaria de agua, durante los distintos periodos de crecimiento, se obtienen mejores cosechas.
| Semana | Estado de crecimiento | Metros cúbicos (m3) necesarios |
|---|---|---|
| 1ª | Siembra | 42 |
| 2ª | Nascencia | 42 |
| 3ª | Desarrollo primario | 52 |
| 5ª | Crecimiento | 120 |
| 8ª | Floración | 185 |
| 9ª | Polinización | 190 |
| 11ª | Fecundación | 200 |
| 12ª | Crecimiento y maduración de la mazorca | 192 |
| 14ª | Semana | 190 |
El aprendizaje de patrones y relaciones es gradual. Toda vez que se ha comprendido, cómo se forman los patrones de repetición, los estudiantes estarán en condiciones de comprender los patrones de recurrencia.
| El manejo de sucesiones permite desarrollar la habilidad para el reconocimiento de patrones y para establecer las relaciones que se dan entre los diferentes elementos.[11] |
Reconocer patrones, una competencia [12][editar | editar código]
Los estudiantes de sexto grado necesitan desarrollar habilidades para reconocer la estructura de los patrones, interpretar las operaciones aritméticas implícitas en patrones, y encontrar las relaciones de causa-efecto en patrones presentes en el ámbito que les rodea.[13]
La identificación de patrones y relaciones contribuye al desarrollo de las habilidades para:
- Analizar y buscar regularidades.
- Organizar y clarificar información.
- Transferir conocimientos y procedimientos de las matemáticas a otras áreas del conocimiento.
- Aprender a razonar de forma lógica e intuitiva (deductivo e inductivo)
- Formular hipótesis, contrastarlas y compararlas para comprobarlas o rechazarlas.
Identificar patrones y relaciones[editar | editar código]
La habilidad para identificar patrones y relaciones se adquiere de manera conjunta en las actividades de la vida diaria.
Los estudiantes deben ser capaces de comprender un patrón, es decir, analizar un patrón y descubrir su estructura de base o núcleo, es decir, la ley según la cual, se construye la sucesión de los elementos y si es posible representarlo matemáticamente.
La Fundación La Ayuda, ofreció donar Q.5.00 por cada libro bien forrado que encontrarán en las aulas de 1º a 6º. Durante la semana nos dedicamos a forrar todos los libros y se obtuvo lo siguiente:
| Grado | 1º | 2º | 3º | 4º | 5º | 6º |
| Libros Forrados | 5 | 15 | 25 | 35 | 45 | 55 |
| Aportación | Q25. | Q75. | ¿? | ¿? | ¿? | ¿? |
¿Cuánto dinero donó la Fundación por lo libros forrados de 6º grado?
| “La búsqueda, construcción y clasificación de patrones promueve el desarrollo del pensamiento lógico.”[15] |
Partir de los conocimientos y experiencias previas[editar | editar código]
Cualquier aprendizaje es más duradero y eficaz si se parte de los aprendizajes y experiencias previas que los estudiantes adquieren en su interacción con las personas, objetos y experiencias sociales de la vida diaria.
Las experiencias ayudan al estudiante a descubrir las regularidades que luego podrán representar, a la vez que les facilitarán la identificación de otras regularidades más complejas.
Juan ayuda a su papá a llenar las cajas de dulces para la venta del fin de semana. Cada caja se vende a Q28.00. Debe colocar la cantidad de dulces según le indican los precios de la tabla:
| Mazapán | Q7.00 cada uno |
| Pepitoria | Q2.33 cada uno |
| Higos | Q1.40 cada uno |
| Quiebradientes | Q0.85 cada uno |
Para no confundirse, Juan elaboró la siguiente tabla, con la cantidad de dulces que debe colocar:
| Mazapán | Pepitorias | Higos | Quiebradientes |
| 1 | 3 | 5 | 7 |
¿Qué haría Juan para elaborar esa tabla?
¿Qué relación hay entre los elementos de la secuencia formada por la cantidad de dulces que contiene cada caja?
Usar material concreto[editar | editar código]
Los estudiantes se interesan y aprenden mejor los conceptos de patrones y relaciones si usan material concreto. Con él tendrán oportunidad de representar los patrones que identifican en la vida real y establecer las correspondientes relaciones.
Identificar patrones y relaciones en situaciones problema[editar | editar código]
La identificación de patrones y relaciones es ideal hacerla desde una situación problema, de forma que los estudiantes tengan la oportunidad de formular hipótesis, comunicar las posibles soluciones, comprobarlas o refutarlas.
| Es importante que los estudiantes se familiaricen con los patrones y relaciones y que aprendan a identificarlas en la vida diaria. |
Habilidades para el aprendizaje de patrones y relaciones[editar | editar código]
- Identificar semejanzas y diferencias Para identificar patrones es importante desarrollar la habilidad de comparación, por la cual los estudiantes distinguirán semejanzas y diferencias para “detectar los rasgos fundamentales que conforman una estructura de aquellos que no son esenciales”.[17]
- Extender y completar un patrón Cuando el estudiante ha comprendido la secuencia que sigue un patrón, podrá describir la secuencia de la serie, introduciendo símbolos; también podrá hacer predicciones acerca del tipo de objeto, figura o elemento que ocupará un lugar dado en la secuencia.
Análisis: Distinción y separación de las partes de un todo hasta llegar a conocer sus principios o elementos.
- Analizar y buscar regularidades La habilidad cognitiva de análisis es necesaria para interpretar y explicar patrones. El estudiante necesita estar expuesto al análisis de patrones, los cuales puede observar en la naturaleza, el entorno sociocultural y también los que le proporcione el docente dentro del aula.
Aprender de lo más fácil a lo más difícil[editar | editar código]
En primer y tercer grados de primaria, los estudiantes aprenden a copiar patrones, identificar la regularidad de patrones sencillos y extender la sucesión de sus elementos y a identificar no solo la repetición o recurrencia de los elementos de patrones más complejos, sino también a explicarlos. En sexto grado, los estudiantes deben aprender a expresarlos de forma simbólica. El aprendizaje de patrones y relaciones debe desarrollarse “a lo largo de todo el año y todos los años de escolaridad, relacionándolos con los otros contenidos que se estén tratando, ya sea de aritmética como de geometría, medida o estadística y probabilidades, no descuidando el poder ejemplificar regularidades con otros contenidos de las áreas de curriculares.”[18]
| Patrones y relaciones no debe enseñarse como un automatismo. Es importante fomentar su comprensión para que encuentren regularidades, interpreten los procesos de formación y los usen con propiedad.[19] |
- ↑ Curriculum Nacional Base. (2008), p. 92.
- ↑ El significado de las palabras que aparecen en el glosario fueron tomadas del Diccionario de la Academia Española.
- ↑ Avances en línea. El mundo matemático. “Las formas.” Recuperado el 13 de abril de 2012, en http://www.project2061.org/esp/publications/bsl/online/ch9/ch9.htm#Shapes
- ↑ Curriculum Nacional Base, Tercer grado del Nivel Primario. Indicador de logro 1.4. del área de Matemá-ticas, p. 101.
- ↑ Godino, J. y Font, V. (2003) Razonamiento algebraico y su didáctica para maestros. P. 774.
- ↑ Cfr. Brassan, A.; Bogisic, B. (1996). Las regularidades: fuente de aprendizajes matemáticos, p. 3.
- ↑ “La germinación de una semilla I”. (Noviembre, 2006). El rincón de la ciencia. No 38. Recuperado el 23 de abril de 2012, en http://centros5.pntic.mec.es/ies.victoria.kent/Rincon-C/Alumnos/al-22/al-22.htm
- ↑ Godino, J. y Font, V. (2003) Op. Cit., p. 774.
- ↑ Para desarrollar este tema se tomó como base los documentos: Las regularidades; fuente de aprendizajes matemáticos y El proceso de matematización progresiva en el tratamiento de patrones.
- ↑ Curriculo Nacional Base (2008). Op. Cit., p. 101.
- ↑ De Faria. (s.f.) p. 6.
- ↑ Para desarrollar este tema se tomó como base el documento Las regularidades: Fuente de aprendizajes matemáticos.
- ↑ Cfr. Curriculum Nacional Base. Op.cit., p. 101.
- ↑ http://pedagogas.wordpress.com/2008/05/27/material-concreto/
- ↑ De Faria, E. (s.f.) Formación continua: 2011. Materiales para el primer ciclo. PDF.
- ↑ name="Comparar">http://es.thefreedictionary.com/comparar
- ↑ Brassan, A.; Bogisic, B. (1996). Op. Cit., p. 8.
- ↑ Brassan, A.; Bogisic, B. (1996) Ibídem, p. 8.
- ↑ Brassan, A.; Bogisic, B. (1996). Ibídem, p. 8.
Conjunto de experiencias, planificadas o no, que tienen lugar en los centros educativos como posibilidad de aprendizaje del alumnado. Una perspectiva tradicional acentúa el carácter de plan (con elementos como objetivos, contenidos, metodología y evaluación), frente a un enfoque práctico que destaca las experiencias vividas en el proceso educativo.
Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.
Conjunto de sonidos articulados con que el hombre manifiesta lo que piensa o siente (DRAE). Facultad que sirve para establecer comunicación en un entorno social, se le considera como un instrumento del pensamiento para representar, categorizar y comprender la realidad, regular la conducta propia y de alguna manera, influir en los demás.
Capacidad o destreza para hacer algo bien o con facilidad.
Destrezas fonológica que consiste en encontrar similitudes y diferencias entre los fonemas o sílabas que forman una palabra.
Destrezas fonológica que consiste en dividir los fonemas o sílabas de una palabra.