Los rompecabezas de Rosita
| (No se muestran 7 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
{{Título}} | {{Título}} | ||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(65).png|right|250px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(65).png|right|250px]] | ||
| + | <center><div style="background-color:#6ea31a; border-radius:10px; float:right; width:225px; color:white; padding:5px; clear:right;"> | ||
| + | <big>'''Instructivo'''</big></div></center> | ||
__TOC__ | __TOC__ | ||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
| Línea 38: | Línea 40: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(66.1).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(66.1).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 56: | Línea 58: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(66.2).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(66.2).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 74: | Línea 76: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.1).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.1).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 89: | Línea 91: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.2).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.2).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 104: | Línea 106: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.3).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(67.3).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 120: | Línea 122: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.1).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.1).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 136: | Línea 138: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.2).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.2).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 158: | Línea 160: | ||
</div> | </div> | ||
<div style="width:60%: float:right;"> | <div style="width:60%: float:right;"> | ||
| − | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.3).png|right| | + | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(68.3).png|right|200px]] |
</div> | </div> | ||
</div> | </div> | ||
| Línea 189: | Línea 191: | ||
*Cuando alguien responda de manera equivocada pregunte por qué escribió esa respuesta y explique por qué esa no es la respuesta correcta. Corrija los errores sin herir la estima de nadie haciéndoles ver que los errores sirven para aprender. | *Cuando alguien responda de manera equivocada pregunte por qué escribió esa respuesta y explique por qué esa no es la respuesta correcta. Corrija los errores sin herir la estima de nadie haciéndoles ver que los errores sirven para aprender. | ||
| − | <big>''' | + | <div style="background-color:#6ea31a; border-radius:2px; width:100%; padding:5px; color:#fff; margin:1em auto 1em auto;"> <big>'''Para pensar y resolver'''</big></div> |
| − | + | [[Archivo:Serie Kemon Ch'abäl estrella verde.png|right|125px]] | |
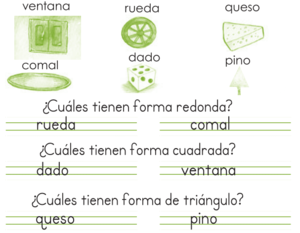
| + | <big>'''A. Observa los dibujos. Luego contesta las preguntas''' </big> | ||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.1).png|left|300px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.1).png|left|300px]] | ||
| − | |||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
| − | <big> '''B. | + | <big> '''B. Identifica las formas y píntalas.'''</big> |
| − | |||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.2).png|left|300px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.2).png|left|300px]] | ||
| − | |||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
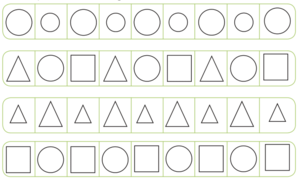
| − | <big>'''C | + | <big>'''C. Observa las figuras geométricas y dibuja las que deben seguir.''' </big> |
| − | |||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.3).png|left|300px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.3).png|left|300px]] | ||
| − | |||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
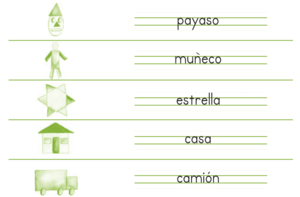
| − | <big>'''D | + | <big>'''D. Escribe ¿Qué figuras formó Rosita? |
| − | payaso - muñeco - estrella - casa - camión </big | + | payaso - muñeco - estrella - casa - camión''' </big> |
| − | |||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.4).png|left|300px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(69.4).png|left|300px]] | ||
| − | |||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
==Taller de reflexión: Los rompecabezas de Rosita== | ==Taller de reflexión: Los rompecabezas de Rosita== | ||
| + | |||
'''Propósito''' | '''Propósito''' | ||
| + | |||
Con las figuras geométricas construyo lo que veo a mi alrededor. | Con las figuras geométricas construyo lo que veo a mi alrededor. | ||
| − | '''Material'' | + | '''Material''' |
| + | |||
Hojas en blanco, lápiz, crayones, papel construcción de colores y una muñeca para simular que es Rosita. | Hojas en blanco, lápiz, crayones, papel construcción de colores y una muñeca para simular que es Rosita. | ||
| − | '''Ideas clave'' | + | '''Ideas clave''' |
*Los rompecabezas al igual que otros juegos educativos son de mucha utilidad porque fomentan la creatividad, el desarrollo de las capacidades de análisis y síntesis, la visión espacial, las estructuras y los movimientos geométricos, son entretenidos y resultan divertidos. | *Los rompecabezas al igual que otros juegos educativos son de mucha utilidad porque fomentan la creatividad, el desarrollo de las capacidades de análisis y síntesis, la visión espacial, las estructuras y los movimientos geométricos, son entretenidos y resultan divertidos. | ||
*Parece, por ello, muy conveniente utilizar estos juegos por sus aspectos motivadores y formativos en el desarrollo del pensamiento lógico donde, además, se puede profundizar aún más en otros aspectos algebraicos, analíticos y estructurales relacionados con otras ramas de las matemáticas. | *Parece, por ello, muy conveniente utilizar estos juegos por sus aspectos motivadores y formativos en el desarrollo del pensamiento lógico donde, además, se puede profundizar aún más en otros aspectos algebraicos, analíticos y estructurales relacionados con otras ramas de las matemáticas. | ||
| − | + | '''1. Para recordar (15 minutos)''' | |
*Distribuya el aula en círculo y muéstreles la muñeca. | *Distribuya el aula en círculo y muéstreles la muñeca. | ||
*Explique: Rosita vino hoy a la clase porque quiere saber que les parecieron sus rompecabezas. Pase la muñeca de mano en mano al ritmo de aplausos. A una señal pare la muñeca y quien se quedó deberá responder a la pregunta: ¿Qué le dirías a Rosita sobre sus rompecabezas? | *Explique: Rosita vino hoy a la clase porque quiere saber que les parecieron sus rompecabezas. Pase la muñeca de mano en mano al ritmo de aplausos. A una señal pare la muñeca y quien se quedó deberá responder a la pregunta: ¿Qué le dirías a Rosita sobre sus rompecabezas? | ||
*Repita el juego unas cuantas veces. Luego siéntense en grupos para realizar la siguiente actividad. | *Repita el juego unas cuantas veces. Luego siéntense en grupos para realizar la siguiente actividad. | ||
| − | + | '''2. Los rompecabezas de la clase (30 minutos)''' | |
Esta actividad consiste en dibujar figuras geométricas y formar otras más complejas. Para ello realice lo siguiente: | Esta actividad consiste en dibujar figuras geométricas y formar otras más complejas. Para ello realice lo siguiente: | ||
| Línea 241: | Línea 240: | ||
''casa y otra que imaginen. '' | ''casa y otra que imaginen. '' | ||
| − | <gallery widths= | + | <center><gallery widths=150px heights=150px> |
Archivo:Serie Kemon Ch'abäl Primer Grado p(71.1).png | Archivo:Serie Kemon Ch'abäl Primer Grado p(71.1).png | ||
Archivo:Serie Kemon Ch'abäl Primer Grado p(71.2).png | Archivo:Serie Kemon Ch'abäl Primer Grado p(71.2).png | ||
| − | </gallery> | + | </gallery></center> |
'''Puede continuar dando instrucciones como las siguientes:''' | '''Puede continuar dando instrucciones como las siguientes:''' | ||
| Línea 252: | Línea 251: | ||
*Concluya la actividad colocando las figuras en una pared. | *Concluya la actividad colocando las figuras en una pared. | ||
Reflexione sobre lo siguiente: | Reflexione sobre lo siguiente: | ||
| + | |||
¿Les gustó hacer rompecabezas?, ¿por qué? | ¿Les gustó hacer rompecabezas?, ¿por qué? | ||
| + | |||
¿En qué se parece lo que acaban de hacer con el contenido de la lectura? | ¿En qué se parece lo que acaban de hacer con el contenido de la lectura? | ||
| − | + | ||
[[Archivo:Serie Kemon Ch'abäl Primer Grado p(72).png|center|300px]] | [[Archivo:Serie Kemon Ch'abäl Primer Grado p(72).png|center|300px]] | ||
| − | |||
<div style="clear:both"></div> | <div style="clear:both"></div> | ||
| + | [[Categoría:Educación Bilingüe]] | ||
Revisión actual del 05:55 20 feb 2018
.png)
Antes de leer[editar | editar código]
Active los conocimientos previos
Pregunte: ¿Saben qué es un instructivo?
Explique: Es la lectura que nos va indicando lo que debemos hacer paso a paso. Por ejemplo, si queremos armar un juguete debemos leer un instructivo que nos muestra cómo armarlo. También, si queremos llegar a un lugar que no conocemos podemos hacer un instructivo del camino por donde debemos ir. Pida que alguien explique cómo llegar a su casa.
Indique que leerán un instructivo.
Pregunte: ¿Qué ven en la primera página?, ¿Qué dice el título? Dé tiempo para que lean el título y luego continúe:
Esta lectura se llama «Los rompecabezas de Rosita». ¿Saben que es un rompecabezas?, ¿Les gustan los rompecabezas?, ¿Qué tenemos que hacer para armar un rompecabezas?
Explique y pregunte: Observen las siguientes imágenes y respondan: ¿Quién será Rosita?, ¿Qué creen que hará Rosita con sus rompecabezas?
Durante la lectura[editar | editar código]
Lectura en voz alta
Explique que usted leerá cada una de las oraciones mientras ellos y ellas observan las imágenes.
Realice las preguntas que se indican a continuación para leer las imágenes y luego lea la oración.
Pregunte: ¿Quién es esa niña? ¿a dónde creen que va?, ¿cómo lo saben? Lea la oración. Explique: Señalen la oración y lean las palabras
Rosita tiene 7 años. Va a la escuela y está en primero.
.png)
Pregunte: ¿Qué ven en la segunda imagen?, ¿dónde están?, ¿qué están haciendo?, ¿quiénes son el niño y la niña?, ¿cómo se sienten?
Lea la oración.
Explique: Señalen la oración y lean las palabras. Pregunte: ¿Qué figuras creen que armará Rosita?
Le gusta mucho armar figuras con sus piezas de cartón. Tiene círculos, cuadrados, triángulos y rectángulos.
.png)
Explique y pregunte: Observen la tercera imagen ¿qué ven?, ¿qué figuras identifican?, ¿qué podría hacer Rosita con estas figuras?
Lea la oración.
Explique: Señalen la oración y lean las palabras.
¿Quieres jugar con ella? Con estas piezas armó la cara de un payaso.
.png)
Explique y pregunte: Vean la cuarta imagen ¿aué observan?, ¿qué figuras identifican?, ¿qué pueden armar con estas figuras? Lea la oración.
Explique: Señalen la oración y lean las palabras.
Con estas piezas armó un niño. Dibújale la carita como más te guste, triste o feliz.
.png)
Pregunte: ¿Qué figuras observan?,¿qué pueden armar con estas piezas?
Lea la oración.
Explique: Señalen la oración y lean las palabras.
Con estas piezas armó una estrella.
.png)
Pregunte: ¿Qué ven en esta imagen?,¿qué creen que se puede armar con estas piezas?
Lea la oración.
Explique: Señalen la oración y lean las palabras. Cuando vea este ícono pregunte si comprenden lo que leen.
Con estas piezas armó una casa
.png)
Pregunte: ¿Qué observan?, ¿qué piezas identifican?
Lea la oración.
Explique: Señalen la oración y lean las palabras.
Con estas piezas armó un camión.
.png)
Se sugiere realizar la lectura de esta imagen con mucha emoción tratando de transmitir los sentimientos del personaje.
Pregunte: ¿Qué observan?, ¿qué está haciendo Rosita?, ¿dónde está?
Lea la oración.
Explique: Señalen la oración y lean las palabras.
Después de jugar, Rosita observó su mundo. Luego dijo: ¡cuántas cosas puedo hacer con mis piezas de cartón!
.png)
Práctica de lectura individual Explique: Leerán la lectura de manera individual y verificaran si siguieron las instrucciones que están escritas. Es decir, si ayudaron a Rosita a armar los rompecabezas. Pueden leer cada oración las veces que quieran hasta comprender todas las palabras.
Después de leer[editar | editar código]
Converse acerca de la lectura preguntando:
¿De qué trata el instructivo?
¿Quién es el personaje?
¿Qué les gustó más de esta lectura?
¿Por qué creen la lectura se llama «Los rompecabezas de Rosita?
¿Qué ideas tienen después de conocer lo que Rosita hizo con sus piezas de cartón?
Ejercicios de Mi cuaderno para pensar y resolver[editar | editar código]
- Realice los ejercicios de la siguiente manera:
- Explique que los realizarán de manera individual para comprobar si comprendieron la anécdota.
- Realice uno por uno. Lea las instrucciones y dé tiempo para que respondan.
- Vaya verificando cada una de las respuestas en plenaria.
- Si lo considera conveniente y tomando en cuenta el nivel de escritura de los niños, copie las respuestas de los ejercicios A y D en el pizarrón, para que los niños las copien en su cuaderno.
- Cuando alguien responda de manera equivocada pregunte por qué escribió esa respuesta y explique por qué esa no es la respuesta correcta. Corrija los errores sin herir la estima de nadie haciéndoles ver que los errores sirven para aprender.
A. Observa los dibujos. Luego contesta las preguntas
.png)
B. Identifica las formas y píntalas.
.png)
C. Observa las figuras geométricas y dibuja las que deben seguir.
.png)
D. Escribe ¿Qué figuras formó Rosita?
payaso - muñeco - estrella - casa - camión
.png)
Taller de reflexión: Los rompecabezas de Rosita[editar | editar código]
Propósito
Con las figuras geométricas construyo lo que veo a mi alrededor.
Material
Hojas en blanco, lápiz, crayones, papel construcción de colores y una muñeca para simular que es Rosita.
Ideas clave
- Los rompecabezas al igual que otros juegos educativos son de mucha utilidad porque fomentan la creatividad, el desarrollo de las capacidades de análisis y síntesis, la visión espacial, las estructuras y los movimientos geométricos, son entretenidos y resultan divertidos.
- Parece, por ello, muy conveniente utilizar estos juegos por sus aspectos motivadores y formativos en el desarrollo del pensamiento lógico donde, además, se puede profundizar aún más en otros aspectos algebraicos, analíticos y estructurales relacionados con otras ramas de las matemáticas.
1. Para recordar (15 minutos)
- Distribuya el aula en círculo y muéstreles la muñeca.
- Explique: Rosita vino hoy a la clase porque quiere saber que les parecieron sus rompecabezas. Pase la muñeca de mano en mano al ritmo de aplausos. A una señal pare la muñeca y quien se quedó deberá responder a la pregunta: ¿Qué le dirías a Rosita sobre sus rompecabezas?
- Repita el juego unas cuantas veces. Luego siéntense en grupos para realizar la siguiente actividad.
2. Los rompecabezas de la clase (30 minutos) Esta actividad consiste en dibujar figuras geométricas y formar otras más complejas. Para ello realice lo siguiente:
- Distribuya el aula en grupos. Proporcióneles cartulina y tijeras. Cada integrante de cada grupo deberá hacer una figura geométrica. Asigne una a cada grupo: cuadrado, círculos, triángulos y rectángulos. Apóyelos en la realización de las figuras.
- Cuando hayan terminado, colóquense en círculo y a una señal deben formar una figura con los de los demás grupos.
- Dé la siguiente instrucción:
Formen grupos de cuatro con quiénes tengan una figura geométrica diferente y construyan una figura con todas ellas, puede ser un árbol, una casa y otra que imaginen.
.png)
.png)
Puede continuar dando instrucciones como las siguientes:
- Busquen compañeros que tengan la misma figura y formen algún objeto o figura.
- Pueden variar el número de integrantes o hacer dos grupos y que entre todos formen figuras.
- Puede también dibujar objetos para formar algo más complejo. Por ejemplo un grupo puede dibujar flores, el otro hojas, otros los tallos y otro una persona. Entre toda la clase pueden armar un jardín. No importa que algunas piezas sean más grandes que las otras. Pueden formar animales asignándole una parte a cada grupo. Por ejemplo: Un grupo dibuja la caras perros, otro colas de perro, otro el cuerpo y otro las patas. Entre todos forman varios perros. Otros ejemplos pueden ser casas, árboles, ropa, personas, etc.
- Concluya la actividad colocando las figuras en una pared.
Reflexione sobre lo siguiente:
¿Les gustó hacer rompecabezas?, ¿por qué?
¿En qué se parece lo que acaban de hacer con el contenido de la lectura?
.png)
En gramática, se entiende por oración a la estructura que está formada por sujeto y predicado. Una oración transmite una idea completa.
Proceso mecánico mediante el cual se aprende a representar palabras y oraciones con la claridad necesaria para que puedan ser leídas por alguien que tenga el mismo código lingüístico. La escritura es la representación gráfica de nuestro lenguaje.