Lectura matemática
m (Editor trasladó la página Serie de Cuadernillos Pedagógicos - Matemáticas/Lectura matemática - Primer grado/Lectura metemática a Serie de Cuadernillos Pedagógicos - Matemáticas/Lectura matemática - Primer grado/Lectura matemática) |
|||
| (No se muestran 5 ediciones intermedias de otro usuario) | |||
| Línea 3: | Línea 3: | ||
=== ¿Qué es la lectura? === | === ¿Qué es la lectura? === | ||
| − | <div style="border:dashed 3px; border-color:#ff3bae; border-radius:6px; margin:2% auto 3% auto; padding:4px; width:83%; color:#ff3bae;"> | + | <div style="border:dashed 3px; border-color:#ff3bae; border-radius:6px; margin:2% auto 3% auto; padding:4px; width:83%; color:#ff3bae; "> |
Lectura es la capacidad de entender un texto escrito<ref name="Ramos">Citados por Ramos, Ena. (enero 2010) en El proceso de la comprensión lectora. Secretos en Red. Recuperado el 28 de febrero de 2012, en http://www.secretosenred.com/articles/2602/1/El-proceso-de-la-comprension-lectora/Paacutegina1.html</ref>. | Lectura es la capacidad de entender un texto escrito<ref name="Ramos">Citados por Ramos, Ena. (enero 2010) en El proceso de la comprensión lectora. Secretos en Red. Recuperado el 28 de febrero de 2012, en http://www.secretosenred.com/articles/2602/1/El-proceso-de-la-comprension-lectora/Paacutegina1.html</ref>. | ||
</div> | </div> | ||
| Línea 17: | Línea 17: | ||
<div style="border:dashed 3px; border-color:#ff3bae; border-radius:6px; margin:2% auto 3% auto; padding:4px; width:83%; color:#ff3bae;"> | <div style="border:dashed 3px; border-color:#ff3bae; border-radius:6px; margin:2% auto 3% auto; padding:4px; width:83%; color:#ff3bae;"> | ||
| − | “La matemática es la ciencia que estudia las propiedades y relaciones que existen entre entes abstractos como números, figuras geométricas o símbolos.”<ref name="Diccionario | + | “La matemática es la ciencia que estudia las propiedades y relaciones que existen entre entes abstractos como números, figuras geométricas o símbolos.”<ref name="Diccionario RAE1">Diccionario de la Real Academia Española. Recuperado el 12 de abril de 2012, en www.rae.es.</ref> |
</div> | </div> | ||
| Línea 43: | Línea 43: | ||
[[Archivo:Cuadernillo3 Mate Primero (8).png|center|200px]] | [[Archivo:Cuadernillo3 Mate Primero (8).png|center|200px]] | ||
| + | |||
| + | {| style="background-color:#ff2b7f; border-radius:10px; margin:2% auto 3% auto; width: 85%; color:white;" | ||
| + | | [[Archivo:Icono rompecabeza transparente.png|right|link=|75px]] | ||
| + | | La matemática también es un lenguaje, por eso puede integrarse con la enseñanza de la lectura. | ||
| + | |} | ||
| + | ------------------------ | ||
| + | <big>'''La lectura matemática es la capacidad por la cual se…'''</big> | ||
| + | |||
| + | <div style="clear:both"></div> | ||
| + | <div style="background-color:#ff2b7f; border-radius:6px; padding:4px; float:right; width:45%; margin:2% auto 3% auto; "> | ||
| + | <center><big>…lee comprensivamente la información que proporciona el planteamiento de un problema para encontrar la solución.</big></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="background-color:#ff2b7f; border-radius:6px; padding:4px; float:left; width:45%; margin:2% auto 3% auto;"> | ||
| + | <center><big>…comprenden los signos empleados, de forma escrita o impresa, propios del lenguaje matemático.</big></center> | ||
| + | </div> | ||
| + | |||
| + | [[Archivo:Cuadernillo3 Mate Primero (9.3).png|left|100px]] | ||
| + | [[Archivo:Cuadernillo3 Mate Primero (9.3).png|right|100px]] | ||
| + | |||
| + | <div style="clear:both"></div> | ||
| + | <div style="border:solid 2px; border-color:#ff2b7f; border-radius:6px; padding:4px; float:left; width:20%; margin:2% auto 3% auto; width:45%; height:110px"> | ||
| + | [[Archivo:Cuadernillo3 Mate Primero (9.4).png|center|400px]] | ||
| + | </div> | ||
| + | |||
| + | <div style="border:solid 2px; border-color:#ff2b7f; border-radius:6px; padding:4px; float:right; width:20%; margin:2% auto 3% auto; width:45%; height:110px"> | ||
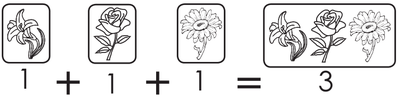
| + | <center><big>En el jardín hay una rosa, un lirio y un girasol. ¿Cuántas flores son? | ||
| + | Un lirio, más una rosa, más un girasol, es igual a tres flores.</big></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="clear:both"></div> | ||
| + | La lectura matemática es especialmente importante para resolver problemas matemáticos, porque requiere del estudiante:<ref name="Cuadernillo no. 1">Según el cuadernillo no. 1 de Resolución de problemas de esta serie.</ref> | ||
| + | |||
| + | [[Archivo:Cuadernillo3 Mate Primero (9.5).png|center|625px]] | ||
| + | |||
| + | == Destrezas lectoras y lectura matemática == | ||
| + | |||
| + | Al leer matemáticas se integran las habilidades básicas de comprensión lectora. | ||
| + | |||
| + | *'''Clarificar:''' Hacer que algo sea más fácil de entender, decirlo de una manera sencilla.<ref name="The Free Diccionary">The Free Diccionary, recuperado en http://es.thefreedictionary.com/clarificar el 10 de abril de 2012.</ref> | ||
| + | *'''Comparar:''' Es fijar la atención en dos o más cosas para encontrar parecidos y apreciar diferencias entre ellas.<ref name="The Free Diccionary2">The Free Diccionary, recuperado en http://es.thefreedictionary.com/comparar el 10 de abril de 2012.</ref> | ||
| + | *'''Inferir:''' “Es sacar una consecuencia o deducir algo de otra cosa.”<ref name="Diccionario RAE">Diccionario de la Real Academia Española. Recuperado el 2 de marzo de 2012, en www.rae.es.</ref> | ||
| + | *'''Predecir:''' Anticiparse a lo que sucederá basándose en la información que se tiene y los conocimientos previos. | ||
| + | *'''Concluir:''' “Determinar y resolver sobre lo que se ha tratado”.<ref name="Diccionario RAE">Diccionario de la Real Academia Española. Recuperado el 2 de marzo de 2012, en www.rae.es.</ref> | ||
| + | |||
| + | |||
| + | {| style="background-color:#ff2b7f; border-radius:10px; margin:2% auto 3% auto; width: 85%; color:white;" | ||
| + | | [[Archivo:Icono clip transparente.png|right|link=|75px]] | ||
| + | | Para leer matemáticas, es importante desarrollar una adecuada comprensión lectora. | ||
| + | |} | ||
== Notas == | == Notas == | ||
Revisión actual del 14:22 23 jun 2020
¿Qué es la lectura?[editar | editar código]
Lectura es la capacidad de entender un texto escrito[1].
El lector entiende o comprende un texto escrito cuando, conforme va leyendo, le da un sentido propio a lo que lee según los conocimientos y experiencias que posee.
¿Qué es la ciencia matemática?[editar | editar código]
“La matemática es la ciencia que estudia las propiedades y relaciones que existen entre entes abstractos como números, figuras geométricas o símbolos.”[3]
También se dice que las “matemáticas son el arte de pensar bien para resolver problemas.”[4]
Las matemáticas tienen símbolos y un vocabulario propio, que los estudiantes deben comprender para desarrollar las competencias matemáticas; esto lo logran si desarrollan competencias lectoras. A la vez, las competencias matemáticas favorecen el desarrollo de las competencias comunicativas.
Si en la lectura, las letras forman palabras que representan conceptos, ideas etc., en las matemáticas los números representan cantidades, patrones o relaciones. Las expresiones numéricas son una forma resumida para transmitir información que puede decirse en muchas palabras o que no puede explicarse usando otro lenguaje.[5]
| La matemática también es un lenguaje, por eso puede integrarse con la enseñanza de la lectura. |
La lectura matemática es la capacidad por la cual se…
La lectura matemática es especialmente importante para resolver problemas matemáticos, porque requiere del estudiante:[6]
Destrezas lectoras y lectura matemática[editar | editar código]
Al leer matemáticas se integran las habilidades básicas de comprensión lectora.
- Clarificar: Hacer que algo sea más fácil de entender, decirlo de una manera sencilla.[7]
- Comparar: Es fijar la atención en dos o más cosas para encontrar parecidos y apreciar diferencias entre ellas.[8]
- Inferir: “Es sacar una consecuencia o deducir algo de otra cosa.”[9]
- Predecir: Anticiparse a lo que sucederá basándose en la información que se tiene y los conocimientos previos.
- Concluir: “Determinar y resolver sobre lo que se ha tratado”.[9]
| Para leer matemáticas, es importante desarrollar una adecuada comprensión lectora. |
Notas[editar | editar código]
- ↑ Citados por Ramos, Ena. (enero 2010) en El proceso de la comprensión lectora. Secretos en Red. Recuperado el 28 de febrero de 2012, en http://www.secretosenred.com/articles/2602/1/El-proceso-de-la-comprension-lectora/Paacutegina1.html
- ↑ Cfr. las palabras que aparecen en el glosario con el diccionario de la Real Academia Española.
- ↑ Diccionario de la Real Academia Española. Recuperado el 12 de abril de 2012, en www.rae.es.
- ↑ Gutiérrez V. A. y Montes de Oca, R. (n.f.) La importancia de la lectura y su problemática en el contexto educativo universitario. El caso de la Universidad Juárez Autónoma de Tabasco. Revista Iberoamericana de Educación. Recuperada el 24 de marzo 2010 http://www.rieoei.org/deloslectores/632Gutierrez.PDF
- ↑ Scott Owen & Greg Corrado. Reading Math: The Why and How (Leyendo matemáticas: ¿Por qué y cómo?)
- ↑ Según el cuadernillo no. 1 de Resolución de problemas de esta serie.
- ↑ The Free Diccionary, recuperado en http://es.thefreedictionary.com/clarificar el 10 de abril de 2012.
- ↑ The Free Diccionary, recuperado en http://es.thefreedictionary.com/comparar el 10 de abril de 2012.
- ↑ 9,0 9,1 Diccionario de la Real Academia Española. Recuperado el 2 de marzo de 2012, en www.rae.es.
Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.
Conjunto de sonidos articulados con que el hombre manifiesta lo que piensa o siente (DRAE). Facultad que sirve para establecer comunicación en un entorno social, se le considera como un instrumento del pensamiento para representar, categorizar y comprender la realidad, regular la conducta propia y de alguna manera, influir en los demás.
Aplicar estrategias para entender y recordar. Implica estar en capacidad de comunicar lo que se ha leído y escuchado.