Recursos en el aula
| (No se muestran 10 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
{{Título}} | {{Título}} | ||
| + | __TOC__ | ||
<div style="width:98%; border-style:dashed; border-color:#f599c1; margin:2px; padding:5px "> | <div style="width:98%; border-style:dashed; border-color:#f599c1; margin:2px; padding:5px "> | ||
'''Propósito''' | '''Propósito''' | ||
| Línea 7: | Línea 8: | ||
==Construcción de ecuaciones más simples== | ==Construcción de ecuaciones más simples== | ||
| − | 1. Lea. | + | '''1. Lea.''' |
| − | <div style="background-color:#fde8f1; width: | + | <div style="background-color:#fde8f1; width:98%; padding:10px; margin: 10px auto 10px auto;"> |
A Laura se le pidió que resolviera la ecuación: '''''5 * (a+2) + 4 = 59'''''. La estrategia de Laura consistió en observar la ecuación completa y reducirla de forma ordenada hasta obtener una ecuación simple. Ella razonó de la siguiente forma. Primero se preguntó qué significa la expresión: '''''5 * (a+2)''''', e infiere que a + 2 se debe multiplicar por 5. Laura se pregunta: '''''¿Cuál es el valor de a+2?''''' Después de algunos intentos concluye lo siguiente: | A Laura se le pidió que resolviera la ecuación: '''''5 * (a+2) + 4 = 59'''''. La estrategia de Laura consistió en observar la ecuación completa y reducirla de forma ordenada hasta obtener una ecuación simple. Ella razonó de la siguiente forma. Primero se preguntó qué significa la expresión: '''''5 * (a+2)''''', e infiere que a + 2 se debe multiplicar por 5. Laura se pregunta: '''''¿Cuál es el valor de a+2?''''' Después de algunos intentos concluye lo siguiente: | ||
</div> | </div> | ||
| Línea 21: | Línea 22: | ||
Por tanto, la igualdad es verdadera: 59 = 59 | Por tanto, la igualdad es verdadera: 59 = 59 | ||
| − | 2. Relacione, compare y contraste la información a través de la práctica. | + | '''2. Relacione, compare y contraste la información a través de la práctica.''' |
*Resuelva las siguientes ecuaciones utilizando el método de Laura. No es permitido usar lápiz y papel. Todo procedimiento debe ser mental. Exponga ante sus compañeros los resultados. | *Resuelva las siguientes ecuaciones utilizando el método de Laura. No es permitido usar lápiz y papel. Todo procedimiento debe ser mental. Exponga ante sus compañeros los resultados. | ||
:(a) 4 (x + 12) + 7 = 87 | :(a) 4 (x + 12) + 7 = 87 | ||
| Línea 28: | Línea 29: | ||
:(d) 22 + <span style="font-size:15px"> <math>\frac {p+8}{3}</math></span>=28 | :(d) 22 + <span style="font-size:15px"> <math>\frac {p+8}{3}</math></span>=28 | ||
| − | <div style="background-color:#fde8f1; width: | + | <div style="background-color:#fde8f1; width:98%; padding:10px; margin: 10px auto 10px auto;"> |
La importancia de la comunicación verbal en la clase de matemática: | La importancia de la comunicación verbal en la clase de matemática: | ||
#Cuando se comunican sus ideas y argumentos sobre la forma de resolver un problema matemático de manera oral o escrita, se aprende a expresarse con claridad y convencimiento. | #Cuando se comunican sus ideas y argumentos sobre la forma de resolver un problema matemático de manera oral o escrita, se aprende a expresarse con claridad y convencimiento. | ||
| Línea 34: | Línea 35: | ||
</div> | </div> | ||
| − | + | ==Juegos de mesa== | |
| − | |||
===Dominó de ecuaciones=== | ===Dominó de ecuaciones=== | ||
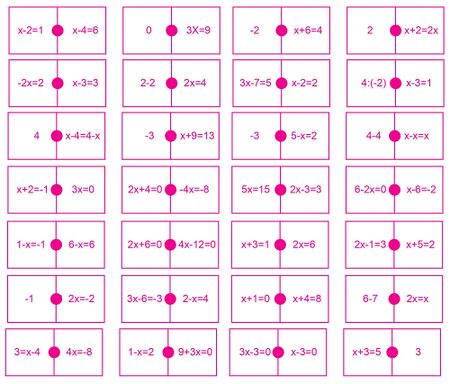
En general, el dominó está formado por fichas rectangulares que tienen puntos que representan un número en particular. Este dominó de ecuaciones que se presenta a continuación, está formado por ecuaciones lineales que se pueden resolver con agilidad mental. Con esta actividad el estudiante juega dominó y al mismo tiempo, resuelve ecuaciones lineales para entregar sus fichas. Esta es una actividad que puede realizarse en grupos de tres integrantes. | En general, el dominó está formado por fichas rectangulares que tienen puntos que representan un número en particular. Este dominó de ecuaciones que se presenta a continuación, está formado por ecuaciones lineales que se pueden resolver con agilidad mental. Con esta actividad el estudiante juega dominó y al mismo tiempo, resuelve ecuaciones lineales para entregar sus fichas. Esta es una actividad que puede realizarse en grupos de tres integrantes. | ||
| Línea 43: | Línea 43: | ||
*Lancen una moneda al aire para organizar quién inicia primero el juego. | *Lancen una moneda al aire para organizar quién inicia primero el juego. | ||
*Gana el primer integrante que se quede sin fichas. | *Gana el primer integrante que se quede sin fichas. | ||
| − | + | [[Archivo:Aprendo y Enseño Conjunto, Sistemas Númericos y Operaciones 1 pag(29).jpg|450px|center]] | |
===Traducción al lenguaje algebraico=== | ===Traducción al lenguaje algebraico=== | ||
El propósito de esta actividad es traducir al lenguaje algebraico relaciones cuantitativas en las que utilizan letras como incógnitas al mismo tiempo que resuelven problemas que involucran ecuaciones de primer grado con una incógnita. Esta es una actividad que puede realizarse en grupos de tres integrantes. | El propósito de esta actividad es traducir al lenguaje algebraico relaciones cuantitativas en las que utilizan letras como incógnitas al mismo tiempo que resuelven problemas que involucran ecuaciones de primer grado con una incógnita. Esta es una actividad que puede realizarse en grupos de tres integrantes. | ||
| Línea 69: | Línea 69: | ||
|- | |- | ||
|style="background:#fff; width:60%; border: 2px solid #ec008d;"|Ana tenia x puntos. | |style="background:#fff; width:60%; border: 2px solid #ec008d;"|Ana tenia x puntos. | ||
| − | |style="background:#fff; width:20%; border: 2px solid #ec008d;"|x | + | |style="background:#fff; width:20%; border: 2px solid #ec008d; text-align:center;"|x |
|style="background:#fff; width:20%; border: 2px solid #ec008d;"| | |style="background:#fff; width:20%; border: 2px solid #ec008d;"| | ||
|- | |- | ||
| Línea 157: | Línea 157: | ||
==Referencias== | ==Referencias== | ||
[[Categoría:Matemáticas]] | [[Categoría:Matemáticas]] | ||
| − | [[Categoría:Básico]] | + | [[Categoría:Básico]][[Category:Book:Pre-álgebra]] |
Revisión actual del 00:23 10 jul 2020
Propósito
Enriquecer el significado de los números y sus operaciones mediante la solución de problemas diversos que impliquen el desarrollo de las habilidades del pensamiento.
Construcción de ecuaciones más simples[editar | editar código]
1. Lea.
A Laura se le pidió que resolviera la ecuación: 5 * (a+2) + 4 = 59. La estrategia de Laura consistió en observar la ecuación completa y reducirla de forma ordenada hasta obtener una ecuación simple. Ella razonó de la siguiente forma. Primero se preguntó qué significa la expresión: 5 * (a+2), e infiere que a + 2 se debe multiplicar por 5. Laura se pregunta: ¿Cuál es el valor de a+2? Después de algunos intentos concluye lo siguiente:
- Como 5 *(a+2) + 4 = 59, entonces 5 *(a+2) tiene un valor de 55, porque 55 + 4 = 59. Esto le permitió construir una ecuación más simple: 5 * (a+2) = 55.
- Luego encontró que (a + 2) debe valer la quinta parte de 55, es decir 11. Esto le permitió reducir la ecuación 5 * (a+2) + 4 = 59, a una ecuación más sencilla: (a + 2) = 11, cuya solución es: a = 9
Laura comprueba que su razonamiento es correcto y verifica:
Ec. original: 5 *(a+2) + 4 = 59, sustituye a = 9 y obtiene: 5 *(9+2) + 4 = 59, que es: 55 + 4 = 55
Por tanto, la igualdad es verdadera: 59 = 59
2. Relacione, compare y contraste la información a través de la práctica.
- Resuelva las siguientes ecuaciones utilizando el método de Laura. No es permitido usar lápiz y papel. Todo procedimiento debe ser mental. Exponga ante sus compañeros los resultados.
- (a) 4 (x + 12) + 7 = 87
- (b) 10 + 3* (y – 8) = 31
- (c) 34 -2 (a-1) = 18
- (d) 22 + [math]\displaystyle{ \frac {p+8}{3} }[/math]=28
La importancia de la comunicación verbal en la clase de matemática:
- Cuando se comunican sus ideas y argumentos sobre la forma de resolver un problema matemático de manera oral o escrita, se aprende a expresarse con claridad y convencimiento.
- Cuando los estudiantes escuchan las explicaciones de otros compañeros tienen oportunidades de desarrollar sus propias interpretaciones y ayudan establecer conexiones lógicas del pensamiento.[1]
Juegos de mesa[editar | editar código]
Dominó de ecuaciones[editar | editar código]
En general, el dominó está formado por fichas rectangulares que tienen puntos que representan un número en particular. Este dominó de ecuaciones que se presenta a continuación, está formado por ecuaciones lineales que se pueden resolver con agilidad mental. Con esta actividad el estudiante juega dominó y al mismo tiempo, resuelve ecuaciones lineales para entregar sus fichas. Esta es una actividad que puede realizarse en grupos de tres integrantes.
Instrucciones:
- Corten las fichas del Cuadro 1. Cada integrante toma 5 fichas y deja 7 fichas sin usar.
- Lancen una moneda al aire para organizar quién inicia primero el juego.
- Gana el primer integrante que se quede sin fichas.
Traducción al lenguaje algebraico[editar | editar código]
El propósito de esta actividad es traducir al lenguaje algebraico relaciones cuantitativas en las que utilizan letras como incógnitas al mismo tiempo que resuelven problemas que involucran ecuaciones de primer grado con una incógnita. Esta es una actividad que puede realizarse en grupos de tres integrantes.
El juego presenta el resultado de un juego de un grupo de personas, entre ellos están: Ana, Isabel, Sergio, Pilar, Marta, Rafael, Teresa, Patricia...
Para determinar los puntos que ha acumulado cada uno en el juego es necesario traducir expresiones algebraicas y resolver ecuaciones.
Instrucciones:
- Se entrega a cada equipo una hoja con la tabla de frases.
- Cada equipo debe traducir las frases a su expresión algebraica. Por ejemplo:
- Ana tenía x puntos. Expresión algebraica: x
- Isabel, el doble de Ana menos 100 puntos. Expresión algebraica: 2x - 100
- Se reparten cinco tarjetas al azar a cada equipo. (Ver Cuadro 2).
- Relacionan las preguntas de las tarjetas con la tabla de frases y resuelven.
- Gana el equipo que termina primero y de forma correcta sus cinco preguntas.
| Frase | Expresión | Expresión reducida |
| Ana tenia x puntos. | x | |
| A Pablo le faltaban 500 puntos para alcanzar a Isabel. | ||
| Sergio consiguió el triple de Ana más 300 puntos. | ||
| Lo de Pilar menos lo de Isabel es 3 veces lo de Ana. Pilar tuvo entonces: | ||
| Marta la quinta parte de lo de Pilar. | ||
| A Rafael le faltan 1000 puntos para tener lo de Sergio. | ||
| Si a Raquel le quitase Ana Belén 500 puntos, tendría como Ana. Raquel tiene: | ||
| Patricio tiene dos veces los de Raquel, más 100 puntos. | ||
| Juntas, Teresa y Patricia, suman tres veces lo de Ana. Teresa tiene: | ||
| Daniel obtuvo la tercera parte de Sergio más 2000 puntos. |
Tarjetas con preguntas relacionadas a la tabla de frases.
| 1. Si Raquel obtuvo 3500 puntos, ¿Cuántos puntos sacó Teresa? | 2. Si Daniel y Pablo juntaron 7500 puntos, ¿Cuántos puntos sacó Isabel? | 3. Si pilar consiguió 4900 puntos, ¿Cuántos tenía Patricia? |
| 4. Si Isabel obtuvo la misma puntuación que Rafael, ¿Cuántos puntos saco Marta? | 5. Si Marta e Isabel juntaron ellas dos 5520 puntos, ¿Cuántos puntos tuvo Daniel? | 6. La puntuación de Isabel menos la de Marta fue de 1320 puntos, ¿Cuántos sacó Teresa? |
| 7. Lo de Pablo menos lo de Rafael fueron 90 puntos, ¿Cuántos puntos sacó Daniel? | 8. Dos veces lo de Ana menos lo de Marta fueron 9020 puntos, ¿Cuántos sacó Raquel? | 9. Sumando lo de Sergio, lo de Pablo y lo de Rafael se obtiene 7000 puntos, ¿cuántos tuvo Patricia? |
| 10. La novena parte de los de Pablo son 600 puntos, ¿Cuántos sacó Ana? | 11. La puntuación de Pilar menos la de Isabel fueron 3600 puntos, ¿Cuántos sacó Sergio? | 12. Teresa y Patricia tuvieron 800 puntos más que Isabel, ¿Cuánto obtuvo Ana? |
| 13. Ocho veces lo de Marta fueron 6240 puntos, ¿Cuántos puntos tuvo Sergio? | 14. Daniel sacó 12100 puntos, ¿Cuántos puntos sacó Patricia? | 15. Tres veces lo de Patricia es 18300 puntos, ¿Cuántos obtuvo Daniel? |
| 16. Lo de Sergio menos lo de Teresa eran 11400 puntos, ¿Cuántos sacó Patricia? | 17. La quinta parte de los de Pilar más lo de Raquel eran 7520 puntos, ¿Cuántos sacó Teresa? | 18. El doble de los puntos de Rafael son 16300, ¿Cuántos puntos sacó Marta? |
| 19. Si Daniel hubiese sacado 400 puntos mas, tendría 12500 puntos, ¿Cuántos puntos sacó Pilar? | 20. Si Roció le regalase 1000 puntos a Marta, entonces este tendría 2980 puntos, ¿Cuántos puntos obtuvo Rafael? | 21. Pablo obtuvo la tercera parte de Daniel ¿Cuántos puntos consiguió Ana? |
| 22. Si a Patricia le diese alguien 1700 puntos más, llegaría a tener cinco veces lo de Pilar. ¿Y Ana cuanto tuvo? | 23. La cuarta parte de los puntos de Marta son 1370 puntos, ¿Cuántos tiene Isabel? | 24. La raíz cuadrada de los puntos de Patricia son 90 puntos, ¿Cuántos saco Rafael? |
| 25. La tercera parte de los puntos de Raquel, aumentado en 450 son 1550, ¿Cuántos puntos sacó Teresa? | 26. Raquel obtuvo cinco veces más puntos que Teresa, ¿Cuántos puntos sacó Ana? | 27. La quinta parte de lo que ha sacado Daniel, más 400 puntos suman 1500, ¿Cuántos puntos sacó Pilar? |
| 28. Lo de Rafael menos lo de Pablo fueron 1650 puntos, ¿Cuántos consiguió Raquel? |
Referencias[editar | editar código]
- ↑ Fuente: Información adaptada de Godino, 2003
Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.
Conjunto de sonidos articulados con que el hombre manifiesta lo que piensa o siente (DRAE). Facultad que sirve para establecer comunicación en un entorno social, se le considera como un instrumento del pensamiento para representar, categorizar y comprender la realidad, regular la conducta propia y de alguna manera, influir en los demás.
Un grupo de personas que trabajan hacia una meta común para el cual todos son mutuamente responsables.