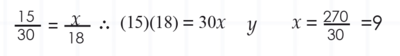15
| (No se muestran 9 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
| − | <span style="font-size:200%;;color: #ff0088">Semejanza de triángulos</span | + | {{#TwitterFBLike:right|like}}<span style="font-size:200%;;color: #ff0088">Semejanza de triángulos</span> |
[[Archivo:SEMENJANZA_DE_TRIANGULOS.png |900px]] | [[Archivo:SEMENJANZA_DE_TRIANGULOS.png |900px]] | ||
== <span style="color: #ff0088;">Presentación</span> == | == <span style="color: #ff0088;">Presentación</span> == | ||
| − | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.</span> | + | <div style="float:right">__TOC__</div> |
| + | <span style="color: #ff0088;">La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del | ||
| + | área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.</span> | ||
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 9: | Línea 12: | ||
| | | | ||
<center>'''OBJETIVOS'''</center> | <center>'''OBJETIVOS'''</center> | ||
| − | * Analizar desde los procesos cognitivos, los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Ciclo de Educación Básica del Nivel de Educación Media. | + | * Analizar desde los procesos cognitivos, los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Ciclo de Educación Básica del Nivel de Educación Media. |
* Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | * Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes. | ||
|} | |} | ||
|} | |} | ||
| + | |||
== <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | == <span style="color: #ff0088;">¿Cómo usar este documento?</span> == | ||
| − | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media. En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta aprendizaje de la semejanza de triángulos. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza matemática que el estudiante adquiere y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. En el apartado '''Análisis del error''', se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. | + | Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media. |
| − | Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde | + | |
| − | luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | + | En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta aprendizaje de la semejanza de triángulos. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza matemática que el estudiante adquiere y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. |
| + | |||
| + | En el apartado '''Análisis del error''', se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. | ||
| + | |||
| + | La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país. | ||
| + | |||
== <span style="color: #ff0088;">Semejanza de triángulos</span> == | == <span style="color: #ff0088;">Semejanza de triángulos</span> == | ||
Un triángulo es una figura geométrica plana que está formada por tres líneas rectas. Tiene la característica de poseer tres ángulos internos que suman 180°. Decimos que dos triángulos son semejantes si se pueden establecer proporcionalidades entre sus lados. | Un triángulo es una figura geométrica plana que está formada por tres líneas rectas. Tiene la característica de poseer tres ángulos internos que suman 180°. Decimos que dos triángulos son semejantes si se pueden establecer proporcionalidades entre sus lados. | ||
| + | |||
Por ejemplo, los triángulos ABC Y DEF son semejantes si: | Por ejemplo, los triángulos ABC Y DEF son semejantes si: | ||
| − | 1. Sus lados homólogos son proporcionales. | + | : 1. Sus lados homólogos son proporcionales. |
| − | AB: DE = AC : DF = BC : EF | + | |
| − | 2. Sus ángulos correspondientes miden | + | <center><big> AB: DE = AC : DF = BC : EF </big></center> |
| − | igual <A = <D, <B = <E, <C = <F | + | |
| − | Si se divide un triángulo con una recta paralela a un lado, se construyen triángulos semejantes. Por ejemplo, para el triángulo cortado por la recta que pasa por D y E que es paralela al lado AB se da la semejanza entre el triángulo ABC y el triángulo DEC de tal forma que se puede demostrar que sus lados homólogos son proporcionales y sus ángulos iguales. | + | : 2. Sus ángulos correspondientes miden |
| − | + | <center><big> igual <big>∠</big>A = <big>∠</big>D, <big>∠</big>B = <big>∠</big>E, <big>∠</big>C = <big>∠</big>F </big></center> | |
| + | |||
| + | Si se divide un triángulo con una recta paralela a un lado, se construyen triángulos semejantes. Por ejemplo, para el triángulo cortado por la recta que pasa por D y E que es paralela al lado AB se da la semejanza entre el triángulo ABC y el triángulo DEC, de tal forma que se puede demostrar que sus lados homólogos son proporcionales y sus ángulos iguales. | ||
| + | |||
| + | [[Archivo:SEMENJANZA DE TRIANGULOS fig 1.png|center|600px]] | ||
| + | |||
== <span style="color: #ff0088;">Análisis del ítem</span> == | == <span style="color: #ff0088;">Análisis del ítem</span> == | ||
Al incluir ítems de semejanza de triángulos se espera que el estudiante evidencie que utiliza correctamente el cálculo matemático para encontrar el dato que se le solicita. | Al incluir ítems de semejanza de triángulos se espera que el estudiante evidencie que utiliza correctamente el cálculo matemático para encontrar el dato que se le solicita. | ||
| − | + | ||
| + | [[Archivo:SEMENJANZA DE TRIANGULOS fig 2.png|center|400px]] | ||
| + | |||
| + | [[Archivo:SEMENJANZA DE TRIANGULOS fig 3.png|center|400px]] | ||
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| <span style="color: #ffffff;">Porcentaje de respuestas correctas en los ítems que evalúan semejanza de triágulos. '''22,7%'''</span> | | <span style="color: #ffffff;">Porcentaje de respuestas correctas en los ítems que evalúan semejanza de triágulos. '''22,7%'''</span> | ||
|} | |} | ||
La demanda cognitiva de este ítem, ubicada en Análisis, '''requiere del estudiante que identifique similitudes, diferencias y las relaciones importantes que se forman en la semejanza de dos figuras geométricas.''' | La demanda cognitiva de este ítem, ubicada en Análisis, '''requiere del estudiante que identifique similitudes, diferencias y las relaciones importantes que se forman en la semejanza de dos figuras geométricas.''' | ||
| + | |||
{| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | {| style="background:#ff0088;border:1px solid #ff0088;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| | | | ||
| Línea 39: | Línea 59: | ||
Previo a las resolución de problemas que involucren semejanza de triángulos es necesario fortalecer los siguientes temas: | Previo a las resolución de problemas que involucren semejanza de triángulos es necesario fortalecer los siguientes temas: | ||
| − | + | # Clasificación de los triángulos por la medida de sus lados y de sus ángulos | |
| − | + | # Proporciones geométricas | |
| − | + | # Ecuaciones lineales. | |
|} | |} | ||
|} | |} | ||
| Línea 47: | Línea 67: | ||
| | | | ||
| − | El ítem consiste en un triángulo rectángulo con catetos de 15 unidades y 30 unidades | + | El ítem consiste en un triángulo rectángulo con catetos de 15 unidades y 30 unidades. Se traza una línea recta paralela al cateto de 15 unidades y se forma el triángulo rectángulo semejante con catetos de x unidades y 18 unidades. Para determinar el valor de x se escribe la siguiente igualdad por la semejanza de triángulos: |
| − | + | ||
| + | [[Archivo:SEMENJANZA DE TRIANGULOS fig 4.png|center|400px]] | ||
|} | |} | ||
| − | Los posibles errores cometidos por los estudiantes son los siguientes. | + | |
| − | Si el estudiante eligió la opción: | + | Los posibles errores cometidos por los estudiantes son los siguientes. Si el estudiante eligió la opción: |
| − | b. No tiene conocimiento de la semejanza de triángulos y resuelve que el valor del lado x es la diferencia 18 – 12 y obtiene como respuesta 6. | + | |
| − | c. Identifica un triángulo rectángulo y aplica el teorema de Pitágoras determinando la hipotenusa del triángulo mayor obteniendo √302+152 = √1125; este resultado es mayor que 15 de tal forma que se concluye que no relaciona la diferencia de tamaño entre 15 y el lado desconocido x. | + | b. No tiene conocimiento de la semejanza de triángulos y resuelve que el valor del lado x es la diferencia 18 – 12 y obtiene como respuesta 6. |
| − | d. No comprende la semejanza de triángulos debido a que escribe las proporciones de forma incorrecta estableciendo la relación: 18 : 12 = 15 : x, y resuelve que (12)(15) = 18x de donde obtiene que el valor de x es 180/18 = 10 | + | |
| + | c. Identifica un triángulo rectángulo y aplica el teorema de Pitágoras determinando la hipotenusa del triángulo mayor obteniendo √302+152 = √1125; este resultado es mayor que 15, de tal forma que se concluye que no relaciona la diferencia de tamaño entre 15 y el lado desconocido x. | ||
| + | |||
| + | d. No comprende la semejanza de triángulos debido a que escribe las proporciones de forma incorrecta estableciendo la relación: 18 : 12 = 15 : x, y resuelve que (12)(15) = 18x de donde obtiene que el valor de x es 180/18 = 10. | ||
| + | |||
{| style="border:2px solid #ff0088;border-radius: 4px;padding:8px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="65%" | {| style="border:2px solid #ff0088;border-radius: 4px;padding:8px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="65%" | ||
| | | | ||
| Línea 65: | Línea 90: | ||
| | | | ||
| − | En el [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 1]] expresa que el estudiante “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y | + | En el [[Malla curricular de Matemáticas - Tercer Grado#Escrito|competencia 1]] expresa que el estudiante “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y relaciones”. Para ello, se propone como '''indicador de logro''' “la resolución de problemas que involucran cálculo de medidas y aplicación de propiedades de figuras planas y cuerpos sólidos”. Los contenidos declarativos que permitirán desarrollar la competencia prevista son: Medidas relacionadas con figuras planas y cuerpos sólidos. Círculo y segmentos asociados. Tipos de ángulos en el círculo. Tipos de cuerpos sólidos. Propiedades y características de los cuerpos sólidos.<ref>Currículo Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado, 2010, p. 49.</ref> |
| − | <ref>Currículo Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado, 2010, p. 49.</ref> | ||
|} | |} | ||
|} | |} | ||
| + | |||
== <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | == <span style="color: #ff0088;">Sugerencias de estrategias de aprendizaje</span> == | ||
| − | + | # Seleccione 3 triángulos como mínimo para que los estudiantes los dibujen en hojas | |
papel bond: | papel bond: | ||
| − | + | #* Con la ayuda de una regla y transportador midan los lados y ángulos respectivos a cada triángulo. | |
| − | + | #* Tracen una recta paralela a uno de los lados del triángulo y midan los lados y ángulos respectivos del nuevo triángulo formado. | |
| − | + | #* Elaboren una copia del triángulo formado. | |
| − | + | #* Seleccionen uno de los lados de cualquiera de los triángulos formados y representen la proporción que permite establecer la semejanza de los lados homólogos elegidos. Los siguientes modelos le servirán de guía:[[Archivo:SEMENJANZA DE TRIANGULOS fig 5.png|center|700px]] | |
| − | homólogos elegidos. Los siguientes modelos le servirán de guía: | + | # Elabore una hoja de ejercicios de 8 problemas que involucren semejanza de triángulos. Son comunes los problemas que involucran sombras proyectadas por el sol, altura de árboles, edificios adyacentes, profundidad de una piscina entre otros. Divida la hoja en dos partes iguales, en el lado izquierdo escriba el problema elegido y la solución sin especificar detalles y en el espacio del lado derecho indique al estudiante que debe crear un problema similar escribiendo el problema y la solución del mismo. El siguiente ejemplo le sirve de guía: |
| − | + | ||
| − | |||
| − | por el sol, altura de árboles, edificios adyacentes, profundidad de una piscina entre otros. Divida la hoja en dos partes iguales, en el lado izquierdo | ||
| − | escriba el problema elegido y la solución sin especificar detalles y en el espacio del lado derecho indique al estudiante que debe crear un problema | ||
| − | similar escribiendo el problema y la solución del mismo. El siguiente ejemplo le sirve de guía: | ||
<center>[[Archivo:SEMENJANZA DE TRIANGULOS fig 6.png |500px]]</center> | <center>[[Archivo:SEMENJANZA DE TRIANGULOS fig 6.png |500px]]</center> | ||
| + | |||
== <span style="color: #ff0088;">Referencias</span> == | == <span style="color: #ff0088;">Referencias</span> == | ||
<references /> | <references /> | ||
| + | |||
'''Documentos consultados'''<br /> | '''Documentos consultados'''<br /> | ||
| − | Baldor, A. (1997). Geometría plana y del espacio y Trigonometría. Publicaciones Cultural, S.A. de C.V. México D.F. | + | # Baldor, A. (1997). ''Geometría plana y del espacio y Trigonometría''. Publicaciones Cultural, S.A. de C.V. México D.F. |
| − | Centro para la Innovación y Desarrollo de la Educación a Distancia. Matemáticas. | + | # Centro para la Innovación y Desarrollo de la Educación a Distancia. ''Matemáticas''. [http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/semejanza/impresos/quincena6.pdf "Semejanza"]. Págs. 89 - 112. Documento recuperado el 8 de junio de 2012. |
| − | + | # Matemáticas. 4º ESO. [http://www.alcaste.com/departamentos/matematicas/secundaria/Cuarto/06_Semejanza/Ejercicios_resueltos.pdf ''Semejanza de triángulos'']. Tema 6. Documento recuperado el 8 de junio de 2012. | |
[[Category:Matemáticas]] [[Category:Básico]] [[Categoría:Resultados de las evaluaciones]][[Category:Book:Serie_aprender_del_error]] | [[Category:Matemáticas]] [[Category:Básico]] [[Categoría:Resultados de las evaluaciones]][[Category:Book:Serie_aprender_del_error]] | ||
Revisión actual del 21:41 18 nov 2014
Semejanza de triángulos
Presentación[editar | editar código]
La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.
|
¿Cómo usar este documento?[editar | editar código]
Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Ciclo de Educación Básica del Nivel de Educación Media.
En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta aprendizaje de la semejanza de triángulos. A continuación, se presenta un ítem clonado de la prueba de Matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad que el docente ubique el contenido evaluado dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza matemática que el estudiante adquiere y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional.
En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida.
La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.
Semejanza de triángulos[editar | editar código]
Un triángulo es una figura geométrica plana que está formada por tres líneas rectas. Tiene la característica de poseer tres ángulos internos que suman 180°. Decimos que dos triángulos son semejantes si se pueden establecer proporcionalidades entre sus lados.
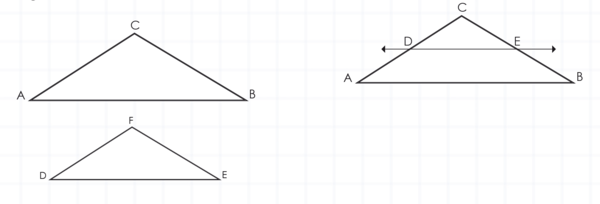
Por ejemplo, los triángulos ABC Y DEF son semejantes si:
- 1. Sus lados homólogos son proporcionales.
- 2. Sus ángulos correspondientes miden
Si se divide un triángulo con una recta paralela a un lado, se construyen triángulos semejantes. Por ejemplo, para el triángulo cortado por la recta que pasa por D y E que es paralela al lado AB se da la semejanza entre el triángulo ABC y el triángulo DEC, de tal forma que se puede demostrar que sus lados homólogos son proporcionales y sus ángulos iguales.
Análisis del ítem[editar | editar código]
Al incluir ítems de semejanza de triángulos se espera que el estudiante evidencie que utiliza correctamente el cálculo matemático para encontrar el dato que se le solicita.
| Porcentaje de respuestas correctas en los ítems que evalúan semejanza de triágulos. 22,7% |
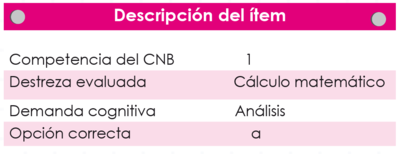
La demanda cognitiva de este ítem, ubicada en Análisis, requiere del estudiante que identifique similitudes, diferencias y las relaciones importantes que se forman en la semejanza de dos figuras geométricas.
|
|
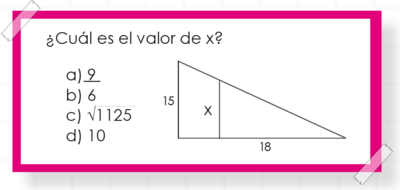
El ítem consiste en un triángulo rectángulo con catetos de 15 unidades y 30 unidades. Se traza una línea recta paralela al cateto de 15 unidades y se forma el triángulo rectángulo semejante con catetos de x unidades y 18 unidades. Para determinar el valor de x se escribe la siguiente igualdad por la semejanza de triángulos: |
Los posibles errores cometidos por los estudiantes son los siguientes. Si el estudiante eligió la opción:
b. No tiene conocimiento de la semejanza de triángulos y resuelve que el valor del lado x es la diferencia 18 – 12 y obtiene como respuesta 6.
c. Identifica un triángulo rectángulo y aplica el teorema de Pitágoras determinando la hipotenusa del triángulo mayor obteniendo √302+152 = √1125; este resultado es mayor que 15, de tal forma que se concluye que no relaciona la diferencia de tamaño entre 15 y el lado desconocido x.
d. No comprende la semejanza de triángulos debido a que escribe las proporciones de forma incorrecta estableciendo la relación: 18 : 12 = 15 : x, y resuelve que (12)(15) = 18x de donde obtiene que el valor de x es 180/18 = 10.
|
En conclusión, los errores evidencian que los estudiantes no tienen conocimiento de la semejanza de triángulos y las proporciones geométricas. |
|
Sugerencias de estrategias de aprendizaje[editar | editar código]
- Seleccione 3 triángulos como mínimo para que los estudiantes los dibujen en hojas
papel bond:
- Con la ayuda de una regla y transportador midan los lados y ángulos respectivos a cada triángulo.
- Tracen una recta paralela a uno de los lados del triángulo y midan los lados y ángulos respectivos del nuevo triángulo formado.
- Elaboren una copia del triángulo formado.
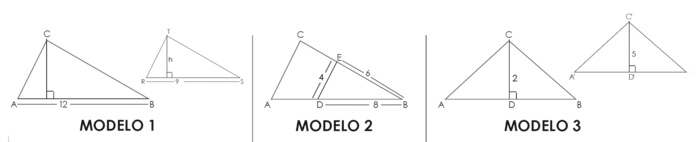
- Seleccionen uno de los lados de cualquiera de los triángulos formados y representen la proporción que permite establecer la semejanza de los lados homólogos elegidos. Los siguientes modelos le servirán de guía:
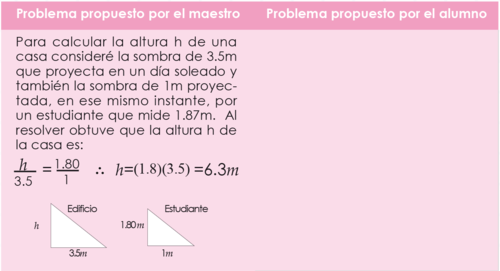
- Elabore una hoja de ejercicios de 8 problemas que involucren semejanza de triángulos. Son comunes los problemas que involucran sombras proyectadas por el sol, altura de árboles, edificios adyacentes, profundidad de una piscina entre otros. Divida la hoja en dos partes iguales, en el lado izquierdo escriba el problema elegido y la solución sin especificar detalles y en el espacio del lado derecho indique al estudiante que debe crear un problema similar escribiendo el problema y la solución del mismo. El siguiente ejemplo le sirve de guía:
Referencias[editar | editar código]
- ↑ Currículo Nacional Base. Nivel de Educación Media, Ciclo Básico, Tercer Grado, 2010, p. 49.
Documentos consultados
- Baldor, A. (1997). Geometría plana y del espacio y Trigonometría. Publicaciones Cultural, S.A. de C.V. México D.F.
- Centro para la Innovación y Desarrollo de la Educación a Distancia. Matemáticas. "Semejanza". Págs. 89 - 112. Documento recuperado el 8 de junio de 2012.
- Matemáticas. 4º ESO. Semejanza de triángulos. Tema 6. Documento recuperado el 8 de junio de 2012.
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Habilidad, facilidad o arte para hacer algo bien hecho.
En el continuo de coaching es el rol de ser muy directo y enseñar, mostrar, guiar, etc.