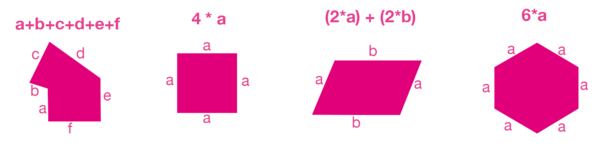Geometría
| Línea 61: | Línea 61: | ||
La figura muestra un rectángulo que tiene una sección sombreada. | La figura muestra un rectángulo que tiene una sección sombreada. | ||
| − | [[Archivo:2 GEOMETRIA-2-figura2.png | | + | [[Archivo:2 GEOMETRIA-2-figura2.png |400px]] |
| + | |||
¿Cuál es el perímetro de la sección sombreada? | ¿Cuál es el perímetro de la sección sombreada? | ||
| Línea 86: | Línea 87: | ||
|'''Contenido evaluado'''||Perímetro | |'''Contenido evaluado'''||Perímetro | ||
|- | |- | ||
| − | |'''Demanda cognitiva''||Utilización | + | |'''Demanda cognitiva'''||Utilización |
|- | |- | ||
| − | |style="background:Grey; color:white"|''' | + | |style="background:Grey; color:white"|'''Respuesta correcta'''||style="background:Grey; color:white"|<u>Opción b</u> |
|} | |} | ||
== <span style="color: #e2007a;">Análisis del error</span> == | == <span style="color: #e2007a;">Análisis del error</span> == | ||
| Línea 115: | Línea 116: | ||
P = 2 (24.5cm + 21cm) | P = 2 (24.5cm + 21cm) | ||
P = 91cm | P = 91cm | ||
| + | == <span style="color: #e2007a;">Sugerencias de estrategias de enseñanza-aprendizaje</span> == | ||
| + | 1. Transformar períodos de clase en tiempos de aulataller, espacios en los que los estudiantes a través de actividades definidas, puedan deducir contenidos | ||
| + | de geometría. Para ello se necesita: a) diseñar una situación problemática que requiera visualizar, explorar, analizar, abstraer propiedades, clasificar, elaborar y validar conjeturas acerca de figuras y sus relaciones; b) elegir un material concreto que facilite el aprendizaje; c) facilitar las indicaciones sin ofrecer rutas de resolución inmediatas; d) dirigir la puesta en común de procedimientos y resultados; e) cerrar la actividad formalizando los contenidos geométricos trabajados. | ||
| + | |||
| + | {| style="background:#e2007a;border:1px solid #e2007a;border-radius: 2px;padding:6px; font-size:100%; line-height:1.2; margin:1em auto 1em auto" width="55%" | ||
| + | | | ||
| + | <span style="color: #ffffff;"> | ||
| + | El razonamiento geométrico puede alcanzarse a través de tareas de conceptualización, investigación y demostración. Estos tres tipos de tareas dentro del enfoque de resolución de problemas, permiten que los estudiantes construyan conocimiento geométrico al resolver situaciones problemáticas (INEE, 2008). | ||
| + | |} | ||
| + | 2. Utilizar elementos del contexto para que los alumnos den sentido al concepto de perímetro. Pueden buscar objetos que tengan silueta de polígonos, medir la longitud de sus lados, calcular el perímetro y dibujar una figura representativa. Por ejemplo pueden medir el campo de futbol (paralelogramo), el tablero del pupitre (cuadrilátero), una fuente con base hexagonal, el patio de la casa, una sección del jardín… Además del cálculo, debe estimularse la generación de ideas sobre las posibles utilidades de conocer el perímetro de los objetos elegidos, de manera que los estudiantes puedan darle significado al aprendizaje y transferir el conocimiento geométrico más allá del salón de clase. | ||
| + | |||
| + | 3. Elaborar un Tangram que consiste en un rompecabezas de origen chino que consta de siete formas básicas obtenidas por la división de un cuadrado y resulta útil como material concreto para aprender distintos teoremas geométricos de figuras planas. Puede hacerse fácilmente utilizando una cartulina (revisar Arenas, | ||
| + | 2012). Utilizando todas las piezas, sin colocar una pieza sobre otra, los estudiantes construyen distintas figuras y responden: | ||
| + | ¿cuál es el perímetro de las figuras?, ¿cuál es la de mayor perímetro?, ¿cuál es la de menor? Se puede alternar entre medidas directas y cálculos a partir | ||
| + | del conocimiento previo de la longitud de los lados de determinadas figuras. | ||
| + | [[Archivo:2 GEOMETRIA-2-figura4.png|400px]] | ||
| + | == <span style="color: #e2007a;">Referencias</span> == | ||
| + | <references /> | ||
| + | |||
| + | * Arenas, M. (2012). Propuesta didáctica para la enseñanza de áreas y perímetros en figuras planas. Obtenido desde http://www.bdigital.unal.edu.co/9300/1/5654114.2012.pdf | ||
| + | * DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras. Guatemala: Ministerio de Educación. | ||
| + | * DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación. | ||
| + | * DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación. | ||
| + | * INEE – Instituto Nacional para la Evaluación de la Educación. La enseñanza de la geometría. México: autor. Jones, K. (2002). Issues in the Teaching and Learning of Geometry. En: Linda Haggarty (Ed.), Aspects of Teaching Secondary Mathematics: perspectives on practice (121-139). London: RoutledgeFalmer. | ||
| + | * Morales, M. y dos Santos, D. (2012). El análisis del contexto de área de figuras planas en los libros didácticos recomendados por el PNLEM. Actas del 3.er Congreso Uruguayo de Educación Matemática. Obtenido desde http://www.semur.edu.uy/curem3/actas/127.pdf | ||
| + | * USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala: autor. | ||
Revisión del 23:27 4 mar 2015
Geometría
Presentación[editar | editar código]
La evaluación es un elemento fundamental en el modelo de la calidad educativa; sin embargo, por sí misma, no mejora los aprendizajes. Es el uso que se haga de los resultados lo que impacta el alcance de las metas educativas del país. Con el objetivo de facilitar la vinculación de los resultados de la Evaluación Nacional de Graduandos con los procesos de enseñanza- aprendizaje que se dan en el aula, la Dirección General de Evaluación e Investigación Educativa –DIGEDUCA– del Ministerio de Educación, plantea este material como un instrumento para que docentes y directores puedan reflexionar acerca de los resultados obtenidos en el 2013. Se espera que esta reflexión incida en la tarea que cada docente realiza en cualquiera de las áreas curriculares del Nivel de Educación Media, del Ciclo de Educación Diversificada.
Evaluación de Graduandos[editar | editar código]
Anualmente todos los estudiantes que cursan el último año del ciclo diversificado participan en la Evaluación Nacional de Graduandos. El objetivo del proceso es determinar el nivel de los aprendizajes alcanzados por los alumnos al finalizar su paso por el sistema educativo. Para medir las habilidades desarrolladas, se evalúan contenidos declarativos y procedimentales en el contexto de competencias básicas para la vida. El área curricular de Matemáticas se incluye en la Evaluación Nacional de Graduandos ya que promueve el desarrollo de los procesos cognitivos necesarios para la comprensión cuantitativa de la realidad. Dentro de esta área se consolidan destrezas relacionadas con análisis, razonamiento y comunicación pertinente y eficaz de ideas, a partir del planteamiento, resolución e interpretación de problemas matemáticos (DIGECADE, 2010; DIGECUR, 2013a; DIGECUR, 2013b). Está vinculada directamente con la competencia básica 3: el uso del pensamiento lógico-matemático para la resolución de problemas de la vida cotidiana. Las pruebas de Matemáticas evalúan contenidos de sistemas numéricos, aritmética, geometría, trigonometría, álgebra, lógica matemática y estadística. En este documento se analizan, desde los procesos cognitivos, errores comunes que los estudiantes evaluados en el 2013 cometieron al resolver ítems de perímetro de figuras geométricas.
|
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participen activamente como miembros de la sociedad. Cfr. USAID, 2009, p. 5. |
¿Cómo usar este documento?[editar | editar código]
Lea la teoría que sustenta y justifica el contenido evaluado. |
Analice el ítem clonado y su descripción. |
A través del análisis del error, identifique posibles debilidades de los estudiantes. |
Decida estrategias a implementar para contribuir al desarrollo de la competencia matemática. |
|
Resultados El porcentaje de respuestas correctas en geometría fue de 21%. Esto quiere decir que si la prueba incluía 5 ítems que evaluaban este contenido, los estudiantes resolvieron correctamente 1.* *El número de ítems varía en las distintas formas de la prueba. |
Gometría[editar | editar código]
Los conocimientos geométricos favorecen el desarrollo de habilidades de visualización, pensamiento crítico, intuición, perspectiva, razonamiento deductivo, razonamiento espacial y argumentación lógica (Jones, 2002). Y en específico, la enseñanza de figuras planas beneficia la capacidad de los estudiantes para resolver problemas prácticos (Morales y dos Santos, 2012).
Entre otros contenidos de geometría, se evalúa el cálculo del perímetro de figuras planas. El perímetro de una figura plana es la suma de las longitudes de sus lados.
Análisis del ítem[editar | editar código]
Resolver correctamente este ítem evidencia que el estudiante es capaz de identificar propiedades de figuras geométricas planas, entiende el concepto de perímetro, reconoce elementos relevantes en gráficos que le ayudan a entender el problema y puede analizar e incorporar aplicaciones de conocimiento geométrico.
|
La figura muestra un rectángulo que tiene una sección sombreada. ¿Cuál es el perímetro de la sección sombreada? a. 515cm b. 91cm c. 45.5cm d. 115cm |
| Competencia básica 3: Pensamiento lógico-matemático | |
| Dimensión clave | Representación cuantitativa y espacial de la realidad. |
| Componente | Formas, patrones y relaciones: establecer propiedades y relaciones entre distintos elementos geométricos. |
| Indicador de logro | Aplica teoremas y conocimientos de geometría plana para interpretar información. |
| Contenido evaluado | Perímetro |
| Demanda cognitiva | Utilización |
| Respuesta correcta | Opción b |
Análisis del error[editar | editar código]
Si seleccionaron la opción a, los estudiantes identificaron la base de la sección sombreada pero calcularon el área del rectángulo (24.5cm * 21cm = 515cm2) en lugar del perímetro y al considerar la respuesta, no tomaron en cuenta las unidades de medida.
Los estudiantes que definieron el perímetro como la opción c, no reconocen el perímetro como la suma de la longitud de todos los lados de la figura y únicamente sumaron la base del área sombreada con su altura (24.5cm + 21cm = 45.5cm).
Quienes eligieron la opción d dominan el concepto del perímetro; sin embargo, no fueron capaces de interpretar el problema planteado en la figura y calcularon el perímetro del rectángulo exterior (2(36.5cm + 21cm) = 115cm) y no el perímetro del rectángulo interior.
b = 36.5cm – 12cm = 24.5cm h = 21cm
P = b + h + b + h P = 2b + 2h P = 2 (b + h)
P = 2 (24.5cm + 21cm) P = 91cm
Sugerencias de estrategias de enseñanza-aprendizaje[editar | editar código]
1. Transformar períodos de clase en tiempos de aulataller, espacios en los que los estudiantes a través de actividades definidas, puedan deducir contenidos de geometría. Para ello se necesita: a) diseñar una situación problemática que requiera visualizar, explorar, analizar, abstraer propiedades, clasificar, elaborar y validar conjeturas acerca de figuras y sus relaciones; b) elegir un material concreto que facilite el aprendizaje; c) facilitar las indicaciones sin ofrecer rutas de resolución inmediatas; d) dirigir la puesta en común de procedimientos y resultados; e) cerrar la actividad formalizando los contenidos geométricos trabajados.
|
El razonamiento geométrico puede alcanzarse a través de tareas de conceptualización, investigación y demostración. Estos tres tipos de tareas dentro del enfoque de resolución de problemas, permiten que los estudiantes construyan conocimiento geométrico al resolver situaciones problemáticas (INEE, 2008). |
2. Utilizar elementos del contexto para que los alumnos den sentido al concepto de perímetro. Pueden buscar objetos que tengan silueta de polígonos, medir la longitud de sus lados, calcular el perímetro y dibujar una figura representativa. Por ejemplo pueden medir el campo de futbol (paralelogramo), el tablero del pupitre (cuadrilátero), una fuente con base hexagonal, el patio de la casa, una sección del jardín… Además del cálculo, debe estimularse la generación de ideas sobre las posibles utilidades de conocer el perímetro de los objetos elegidos, de manera que los estudiantes puedan darle significado al aprendizaje y transferir el conocimiento geométrico más allá del salón de clase.
3. Elaborar un Tangram que consiste en un rompecabezas de origen chino que consta de siete formas básicas obtenidas por la división de un cuadrado y resulta útil como material concreto para aprender distintos teoremas geométricos de figuras planas. Puede hacerse fácilmente utilizando una cartulina (revisar Arenas,
2012). Utilizando todas las piezas, sin colocar una pieza sobre otra, los estudiantes construyen distintas figuras y responden:
¿cuál es el perímetro de las figuras?, ¿cuál es la de mayor perímetro?, ¿cuál es la de menor? Se puede alternar entre medidas directas y cálculos a partir
del conocimiento previo de la longitud de los lados de determinadas figuras.
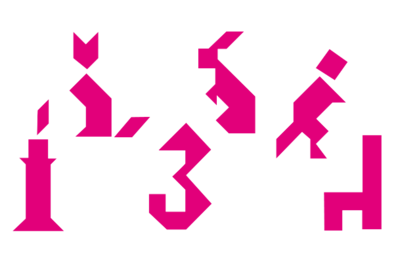
Referencias[editar | editar código]
- Arenas, M. (2012). Propuesta didáctica para la enseñanza de áreas y perímetros en figuras planas. Obtenido desde http://www.bdigital.unal.edu.co/9300/1/5654114.2012.pdf
- DIGECADE –Dirección General de Gestión de Calidad Educativa–. (2010). Curriculum Nacional Base: Bachillerato en Ciencias y Letras. Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013a). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Educación de Productividad y Desarrollo. Guatemala: Ministerio de Educación.
- DIGECUR – Dirección General de Currículo–. (2013b). Curriculum Nacional Base: Bachillerato en Ciencias y Letras con orientación en Finanzas y Administración. Guatemala: Ministerio de Educación.
- INEE – Instituto Nacional para la Evaluación de la Educación. La enseñanza de la geometría. México: autor. Jones, K. (2002). Issues in the Teaching and Learning of Geometry. En: Linda Haggarty (Ed.), Aspects of Teaching Secondary Mathematics: perspectives on practice (121-139). London: RoutledgeFalmer.
- Morales, M. y dos Santos, D. (2012). El análisis del contexto de área de figuras planas en los libros didácticos recomendados por el PNLEM. Actas del 3.er Congreso Uruguayo de Educación Matemática. Obtenido desde http://www.semur.edu.uy/curem3/actas/127.pdf
- USAID –United States Agency for International Development–. (2009). Competencias básicas para la vida. Guatemala: autor.
Indicadores de éxito de un plan escrito en forma específica.
Conjunto de aprendizajes (conocimientos, procedimientos y actitudes) imprescindibles y fundamentales para que todas las personas se realicen personalmente, se incorporen a la vida adulta de manera satisfactoria y participaen activamente como miembros de la sociedad.
Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario
Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.