Guías para resolver la prueba diagnóstica de docentes/¿Qué debo saber para realizar la prueba de Matemática?

En este documento encontrará la lista de temas que conviene estudiar para resolver la prueba diagnóstica de docentes de Matemática.

Objetivo del documento

Proporcionar una lista de temas para que el docente refuerce los conocimientos a los que estará expuesto en la prueba diagnóstica del área curricular de Matemática.

La importancia de evaluar Matemática

La razón por la que se evalúa matemática es porque conforma una herramienta más en la construcción del aprendizaje, donde la abstracción se empieza a exteriorizar por medio del pensamiento, con la capacidad de seguir procesos ordenados y estructurados, necesarios para planificar estrategias en la solución de problemas para la vida en sociedad, interpretar y comunicar la información recopilada en datos. También su aplicabilidad en la mayoría de las ciencias refleja su interés de aprenderla, dominarla y enseñarla. El docente que opte a una plaza en el Ministerio de Educación, debe ser una persona que refleje estas tres características y que además sienta pasión por ella, porque esto permitirá que los estudiantes disfruten el aprendizaje de esta ciencia.

La prueba de Matemática

Es el instrumento que permite identificar el dominio que el docente tiene acerca de los temas de esta área curricular, necesarios para la enseñanza.

Temas de de la prueba

A continuación se presenta una breve descripción de los temas contenidos en la evaluación por cada componente.

Sistemas numéricos y operaciones

Tema	Descripción
Números racionales	Cociente de dos números enteros: Conversión de fracciones a decimales y viceversa Fracciones equivalentes Operaciones básicas con números racionales Problemas que involucran números racionales
Regla de tres	Algoritmo que permite encontrar un término desconocido si se conocen tres datos: Problemas que se resuelven utilizando regla de tres simple Interés simple
Jerarquía de operaciones	Orden para realizar las operaciones: Operaciones combinadas
Valor absoluto y relativo	Valores de los números en una cantidad: Valor posicional Valor de acuerdo al número
Mínimo común múltiplo	Procedimiento que se hace antes de realizar la suma o resta de números racionales con distinto denominador: Mínimo común múltiplo
Números primos	Número natural que tiene exactamente dos divisores: Criterios de divisibilidad
Porcentaje	Fracción de una cantidad que se toma por cada cien contenida en ella: Cálculo del tanto por ciento Problemas que involucran porcentajes
Sistemas de numeración maya	Sistema de numeración de base 20 denominado vigesimal: Conversiones del sistema decimal a maya y viceversa Operaciones básicas con números mayas
Números romanos	Sistema numérico posicional que se basa en siete letras: Conversiones del sistema decimal a romano y viceversa

Matemáticas, ciencia y tecnología

Tema	Descripción
Teoría de conjuntos	Estudio de las propiedades de los conjuntos: Simbología Operaciones entre conjuntos Tipos de conjuntos Formas de expresar conjuntos
Plano cartesiano	Líneas que se cortan en un punto formando ángulos rectos: Identificación de los cuadrantes Localización de puntos en el plano
Calendario gregoriano	Calendario utilizado en casi todo el mundo: Conversiones Operaciones entre unidades de tiempo
Calendario maya	Calendario cíclico basado en movimientos astronómicos: Conversiones de unidades del vigesimal a decimal y viceversa Calendario de la cuenta larga
Equivalencia de unidades	Involucra el uso de equivalencias: Conversiones de unidades de longitud Conversiones de unidades de tiempo
Presupuesto de gastos	Abarca el uso adecuado de operaciones básicas Problemas que involucran gastos, costos y compras
Uso de moneda nacional y extranjera	Involucra el cálculo para realizar conversiones: Problemas de conversión de moneda

Formas, patrones y relaciones

Tema	Descripción
Perímetro	Medida de la orilla de una figura: Perímetro de triángulos Perímetro de rectángulos Perímetro de cuadrados
Área	Espacio que se encuentra comprendido entre ciertos límites: Área de triángulos Área de rectángulos Área de cuadrados
Figuras planas	Aquella que tiene todos los puntos en un plano: Triángulos Rectángulos Cuadrados Conceptos básicos de geometría
Sólidos geométricos	Cuerpos geométricos de figuras tridimensionales: Cono Cilindro Pirámide Esfera Cubo

La incertidumbre, la comunicación y la investigación

Tema	Descripción
Gráficas estadísticas	Análisis e interpretación de datos: Gráficas de barras Gráficas circulares
Medida de tendencia central	Valor central alrededor del cual se concentran los valores de un conjunto de datos observados: Promedio aritmético Moda Mediana

Información acerca de la prueba

A continuación encontrará en forma de pregunta, información acerca de la prueba.

¿Cómo es la prueba?

La prueba de Matemática consta de 50 ítems de selección múltiple. Los docentes cuentan con 60 minutos para resolverla. A continuación se muestra un ejemplo.

¿Cuál es el área de un rectángulo de 15 cm de ancho y 1 m de largo? a) 15 cm2 b) 60 cm2 c) 1 500 cm2 d) 150 cm2

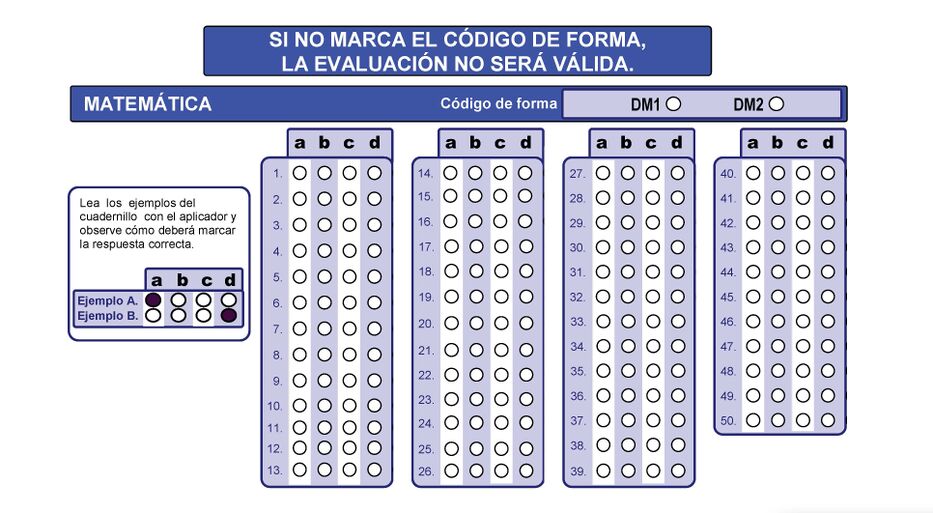
¿En dónde se marcan las respuestas?

En una hoja diseñada para procesamiento electrónico, en la que se selecciona la letra que corresponde a la opción correcta y se rellena completamente el círculo, sin salirse del

contorno. Se requiere el uso de lapicero negro, no gel.

A continuación se muestra una imagen de la hoja para respuestas.

¿Existen otros recursos para ampliar la información acerca de esta evaluación?

En la página web de la Digeduca http://www.mineduc.gob.gt/digeduca/ aparece un espacio dedicado a los docentes; allí encuentra ítems liberados y las soluciones, útiles para familiarizarse con la forma de evaluación.

La siguiente imagen ilustra la página web inicial de la Digeduca.

¿En dónde encuentro más información sobre la prueba de docentes?

En la sección de Preguntas frecuentes sobre la evaluación de docentes, se resuelven dudas sobre la aplicación y otros aspectos importantes.

Término utilizado, a menudo, como un saber hacer. Se suele aceptar que, por orden creciente, en primer lugar estaría la habilidad, en segundo lugar la capacidad, y la competencia se situaría a un nivel superior e integrador. Capacidad es, en principio, la aptitud para hacer algo. Todo un conjunto de verbos en infinitivo expresan capacidades (analizar, comparar, clasificar, etc.), que se manifiestan a través de determinados contenidos (analizar algo, comparar cosas, clasificar objetos, etc.). Por eso son, en gran medida, transversales, susceptibles de ser empleadas con distintos contenidos. Una competencia moviliza diferentes capacidades y diferentes contenidos en una situación. La competencia es una capacidad compleja, distinta de un saber rutinario o de mera aplicación.

Término introducido por Le Boterf, entendido como los conocimientos, procedimientos y actitudes que es preciso emplear para resolver una situación. Unos son recursos internos, que posee la persona, tales como conocimientos, procedimientos y actitudes