Serie Aprender del Error/13

Números racionales

Presentación

La Dirección General de Evaluación e Investigación Educativa del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación. Espera que sea de utilidad a los docentes del área curricular de Matemáticas del Nivel de Educación Media del Ciclo de Educación Básica, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2009.

OBJETIVOS Analizar desde los procesos cognitivos los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Nivel de Educación Media del Ciclo de Educación Básica. Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes.

¿Cómo usar este documento?

Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Nivel de Educación Media del Ciclo de Educación Básica. En primer lugar se ofrece una cápsula informativa acerca de la teoría que sustenta el aprendizaje de los números racionales.

A continuación, se presenta un ítem clonado de la prueba de matemáticas que resuelven los estudiantes de tercero Básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad que el docente identifique este contenido dentro de lo que establece el Curriculum Nacional Base –CNB–, la competencia que se desarrolla por medio de dicho contenido y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional.

En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación. Se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar.

Finalmente se refieren algunas referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.

Números racionales

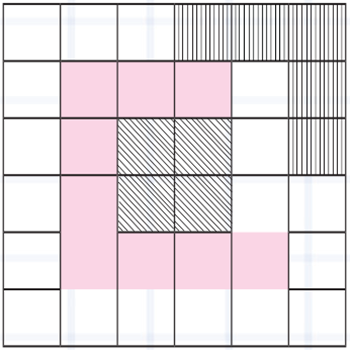
Los números racionales surgen de la necesidad de comparar magnitudes porciones de la unidad, como se muestra en la siguiente figura, que está compuesta por tres diferentes tipos de sombreado. Estas representan las fracciones 5/36, 9/36 y 4/36 del cuadrado total. La parte total sombreada será entonces:

5/36 + 9/36 + 4/36 = 1/2

que representa la mitad del total. De la misma forma se puede representar que la parte sombreada con líneas verticales y diagonales es:

5/36 + 4/36 = 1/4

que representa la cuarta parte del total. Las fracciones se representan mediante figuras geométricas y/o en la recta real, dividiendo la figura o la recta en tantas unidades como indique el denominador y señalando las unidades establecidas en el numerador.

Resolver operaciones con números racionales o fracciones que involucren patrones geométricos requiere un buen dominio de las operaciones de comparación, suma y resta, producto, cociente y simplificación. Por ejemplo:

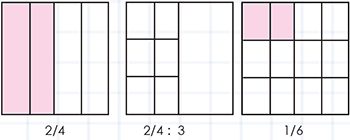
Tres amigos se reparten por igual dos cuartas partes de una caja con dulces. ¿Qué parte de esa fracción le corresponde a cada uno de ellos?

La división de fracciones permite resolver este problema. La secuencia de figuras geométricas mostradas y la división de (2/4) entre 3 indica que a cada amigo le corresponde 1/6 de los dulces que hay en la caja.

Análisis del ítem

Al incluir ítems de números racionales se espera que el estudiante evidencie que utiliza correctamente el pensamiento matemático.

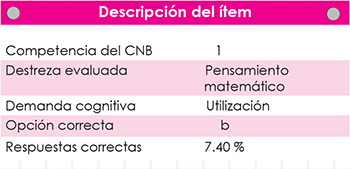
La demanda cognitiva de este ítem, ubicada en Utilización, requiere del estudiante emplea operaciones con números racionales para encontrar la parte representada en una figura geométrica.

Análisis del error

Previo a la enseñanza de este tipo de problemas debe reforzar los conocimientos básicos de los estudiantes en: Representación gráfica de las fracciones Las operaciones de comparación, simplificación de fracciones Las operaciones de suma y resta, producto y división de fracciones.

Los posibles errores cometidos por los estudiantes son los siguientes: si el estudiante eligió la opción…

a. identifica las particiones marcadas en el cuadrado que son 12, pero cuenta las áreas sombreadas que son 4 y expresa que la fracción es 4/12 en lugar de contar las partes no sombreadas, además no considera que las partes no son del mismo tamaño y forma.

b.

c. identifica las particiones marcadas en el cuadrado y observa que son 12, luego cuenta las que no están sombreadas y expresa la fracción 8/12, sin embargo la respuesta es incorrecta porque no considera que las porciones en cada cuadro son de diferente tamaño y forma.

d. divide la figura geométrica en cuatro cuadrados de igual tamaño y suma las fracciones que corresponden al área no sombreada de cada uno de los cuadrados de la forma siguiente: ½ + 1+ 3/2 + ¼ = 13/4. El procedimiento es incorrecto debido a que considera que cada cuadro es una figura independiente que representa la unidad entera.

En conclusión, los errores evidencian que los estudiantes no pueden representar fracciones empleando patrones geométricos y que no tienen conocimiento de las operaciones con fracciones.

En el CNB la competencia 1 expresa que el estudiante “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y relaciones.”. Para ello, se propone como indicador de logro la aplicación de “factorización de polinomios al simplificar fracciones algebraicas y dividir polinomios.”. Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son los Polinomios y sus operaciones y propiedades, Productos Notables, Binomio de Newton, Triángulo de Pascal o de Tartaglia y Factorización.

Sugerencias de estrategias de aprendizaje

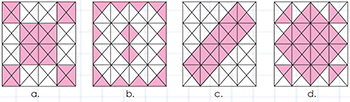
1. Para que el estudiante represente correctamente fracciones, es importante que practique con objetos que puede ver y tocar. Organice a los estudiantes en grupos de 3 personas. Para el desarrollo de esta actividad necesitan dos hojas de papel construcción tamaño carta de diferente color. Sobre una de las hojas debe realizar el rayado que se indica en la figura y luego debe cortarla en las diferentes secciones.

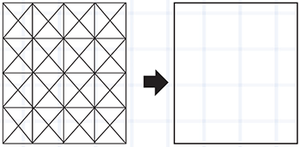
Utilice de fondo la hoja no cortada e indique a los estudiantes que formen los siguientes patrones geométricos de ejemplo que se muestran a continuación, (las figuras presentan un nivel de dificultad medio si lo considera necesario inicie con patrones geométricos sencillos), y luego que escriban la fracción que representa el área sombreada. Promueva la creatividad e ingenio de los estudiantes a formar otros patrones geométricos.

Referencias

Documentos consultados
Caraballo, L. R. Alianza para el Aprendizaje de las Ciencias y las Matemáticas. Mayo 2004. Documento recuperado el 8 de junio de 2012. Disponible en: http://alacima.uprrp.edu/alfa/materiales%20curriculares/Mate_7-9/FraccionesEquivalentes.pdf Salinas García Antonio. Egea Gómez María de Jesús. Fracciones. Documento recuperado el 8 de junio de 2012. Disponible en: http://www.vedoque.com/juegos/matematicas-04-fracciones.swf Santillana Educación SL Matemáticas I ESO. Fracciones.. Documento recuperdo el 8 de junio de 2012. Disponible en: http://www.iesprofesorjuanbautista.es/IMG/ pdf_3-Fracciones.pdf

Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario

Destrezas fonológica que consiste en encontrar similitudes y diferencias entre los fonemas o sílabas que forman una palabra.

Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.

Proceso por el cual las personas adquieren cambios en su comportamiento, mejoran sus actuaciones, reorganizan su pensamiento o descubren nuevas maneras de comportamiento y nuevos conceptos e información.