9

Álgebra: ecuaciones

Presentación

La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Nivel de Educación Media, del Ciclo de Educación Básica, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2009

OBJETIVOS Analizar desde los procesos cognitivos los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Nivel de Educación Media, del Ciclo de Educación Básica. Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes.

¿Cómo usar este documento?

Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Nivel de Educación Media, del Ciclo de Educación Básica. En primer lugar se ofrece una cápsula informativa, acerca de la teoría que sustenta el aprendizaje de las ecuaciones. A continuación, se presenta un ítem clonado de la prueba de matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad de que el docente ubique el contenido dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza que apoya el desarrollo de la competencia matemática y el porcentaje de ítems que fueron resueltos correctamente a nivel nacional. En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación, se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar. Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.

Álgebra: ecuaciones

Para definir una ecuación es necesario iniciar estableciendo qué es una igualdad; esta es una expresión comparada con otra a través de un signo igual (=). Una ecuación es una igualdad entre dos expresiones que cumple con el requisito indispensable de ser verdadera. Las ecuaciones suelen utilizarse en el álgebra para encontrar un valor desconocido llamada incógnita. Considere la ecuación lineal 5 + x = 6 + 1, aparece un valor desconocido la variable “x”, este valor tiene que ser 2 para que la igualdad sea verdadera. Por lo que la solución de la ecuación lineal es x = 2. La ecuación lineal 3x + 3 = 2x + 8 se resuelve elaborando una lista de ecuaciones equivalentes cada una de las mismas más simple que la precedente, los pasos para resolver la ecuación anterior se puede visualizar a continuación:

Análisis del ítem

Al incluir ítems de ecuaciones se espera que el estudiante evidencie que aplica los cálculos necesarios para resolverlas.

En la ecuación x = 86.5 – 0.004t ¿Cuál es el valor de t si x = 68.5? a. 38750 b. 86.496/68.5 c. 7200 d. 4500

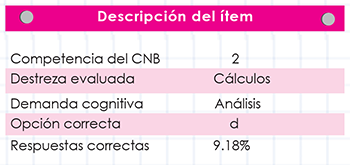
La demanda cognitiva de este ítem, ubicada en Análisis, requiere del estudiante recordar los procedimientos para encontrar la incógnita en una ecuación y aplicar los cálculos correspondientes.

Análisis del error

Previo a la enseñanza de las ecuaciones deben reforzar los siguientes conocimientos básicos: Propiedades de los números reales. Operaciones de suma, resta, multiplicación y división de racionales. Operaciones de suma, resta, multiplicación y división con polinomios. Evaluación de una expresión algebraica.

Los posibles errores cometidos por los estudiantes son los siguientes:

Si el estudiante eligió la opción…

a. comprende que debe sustituir 68.5 en x, y realiza la operación 86.5 + 68.5 =155, pero no aplica correctamente la ley de inversos aditivos, luego efectúa la operación 155/ 0.004 = 38 750.

b. no aplica correctamente la jerarquía de operaciones al realizar la operación 86.5 – 0.004 = 86.496 y expresa la ecuación x = 86.496t pero esta igualdad no es equivalente a la ecuación original. Despeja t empleando la ley del inverso multiplicativo y obtiene el cociente indicado 6.496/68.5 como solución.

c. sustituye 68.5 en x y aplica la propiedad de los inversos aditivos expresando la ecuación equivalente: - 18 = - 0.004t, pero opera incorrectamente el cociente –18/-0.004 resolviendo (18x4)∙(100) y obtiene como resultado 7200.

En conclusión, los errores evidencian que los estudiantes no resuelven ecuaciones lineales por desconocimiento de la ley del inverso aditivo y multiplicativo, cálculos incorrectos con operaciones que involucran el sistema de numeración decimal y aplicación de la notación científica.

En el CNB la competencia 2 expresa que el estudiante “Construye modelos matemáticos en la representación y análisis de relaciones cuantitativas”. Para ello, se propone como indicador de logro la utilización de “diferentes métodos en la resolución de ecuaciones, inecuaciones y sistemas de ecuaciones”. Los contenidos declarativos y procedimentales que permitirán desarrollar la competencia prevista son las Ecuaciones de segundo grado (cuadráticas), Intervalo abierto y el intervalo cerrado, Sistemas de ecuaciones lineales de dos y tres variables, Solución de sistemas de ecuaciones por los métodos: gráfico, sustitución, igualación, eliminación y combinación lineal. Aplicación de sistemas de ecuaciones en la solución de situaciones reales.

Sugerencias de estrategias de aprendizaje

1. Se sugiere que se establezca un proceso de solución con los siguientes pasos:

a. Identificar la variable que se va a trabajar.

b. Aplicar las propiedades de inversos aditivos para dejar la variable en un solo miembro de la igualdad.

c. Reducir los términos semejantes.

d. Aplicar las propiedades de inversos multiplicativos con el fin de dejar sola la variable (despejar la variable).

e. Realizar la comprobación

2. Realizar ecuaciones en forma gradual de dificultad, que involucren fracciones, números decimales, notación científica, operaciones indicadas de suma, resta, multiplicación y división de polinomios sencillos, proporcionar por lo menos 2 o 3 ejercicios de cada nivel de dificultad. Emplear diferentes variables, por ejemplo m, t, y, z; para que el estudiante pueda aplicar el procedimiento indistintamente de la variable y evite memorizar procedimientos. Los siguientes ecuaciones son ejemplos que puede utilizar de guía:
(2x+4) = x+19 , 4(t +10) = 6(2 - t) -6t, 2(2h – 3) = 6+h 3. Seleccione ecuaciones que resuelvan un problema en particular. Elija como mínimo 10 planteamientos y la ecuación respectiva que resuelve el problema. Existe una variedad de temas que puede abordar, como por ejemplo la relación entre las escalas de temperatura ^oC y ^oF se establece por la ecuación: ⁰C = 5/9 ( ⁰F - 32), sí la temperatura corporal del ser humano en escala Celcius es 370 C, ¿cuál es la temperatura corporal en ⁰F?. Recuerde que lo importante es resolver la ecuación formulada y que el estudiante vincule sus conocimientos con otras ciencias. Al resolver sustituye 37^o C en la ecuación planteada y obtiene: multiplicando ambos lados pory se obtiene:(37)=⁰F Suma 32 en ambos lados de la igualdad:o F= 66.6 + 32 = 98.6
Conclusión: la temperatura corporal del ser humano en ^oF es: 98.6

Referencias

Documentos consultados
Aponte, G. (1998). Fundamento de Matemáticas Básicas. Primera Edición. Serie AWLI. Addison Wesley Longman. Mexico.487p.
Swokowsky, E.W y Cole, J.A. (1998). Algebra y Trigonometría. 9ed. International Thomson Editores. México. Pag. 49 – 119
Rodríguez, J. Caraballo, A. Cruz, T. Hernández O.(1997). Razonamiento Matemático. Fundamentos y aplicaciones. Thomson Editores SA. México. Pag. 101 – 127
Astorga, A. y Rodríguez, J. (1984) Capítulo 3: El conjunto de los números reales. Instituto tecnológico de Costa Rica. Escuela de Matemática. Revista digital Matemática, educación e internet. Costa Rica. Recuperado el 8 de junio de 2012 http://www.cidse.itcr.ac.cr/cursos-linea/MATEGENERAL/t2-ecuaciones/pdf/Ecuaciones.pdf
González, J. (s. f) Ecuaciones de primer y segundo grado. Documento recuperado el 8 de junio de 2012 http://thales.cica.es/files/glinex/practicasglinex05/matematicas/ecuaciones/practica.pdf

Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario

Habilidad, facilidad o arte para hacer algo bien hecho.

Destrezas fonológica que consiste en cambiar un fonema por otro.

Conjunto de acciones (formas de actuar o de resolver tareas), con un orden, plan o pasos, para conseguir un determinado fin o meta. Se trata de saber hacer cosas, aplicar o actuar de manera ordenada para solucionar problemas, satisfacer propósitos o conseguir objetivos. Forman los contenidos procedimentales.

En el continuo de coaching es el rol de ser muy directo y enseñar, mostrar, guiar, etc.