10

Exponentes

Presentación

La Dirección General de Evaluación e Investigación Educativa, del Ministerio de Educación, encargada de velar y ejecutar los procesos de evaluación e investigación, para asegurar la calidad educativa, pone en sus manos esta publicación, que espera sea de utilidad a los docentes del área curricular de Matemáticas, del Ciclo de Educación Básica del Nivel de Educación Media, como un instrumento para reflexionar en torno a los resultados de las evaluaciones aplicadas en el año 2013.

OBJETIVOS Analizar desde los procesos cognitivos los errores más comunes en la resolución de los ítems de las pruebas de Matemáticas, aplicadas a los estudiantes de tercer grado del Nivel de Educación Media del Ciclo de Educación Básica. Sugerir a los docentes actividades de enseñanza-aprendizaje que coadyuven al desarrollo de las competencias matemáticas en los estudiantes.

¿Cómo usar este documento?

Para conseguir el objetivo de aprender del error, el presente documento se ha estructurado en tres apartados que se espera sean útiles para mejorar el proceso de aprendizaje de los estudiantes del Nivel de Educación Media del Ciclo de Educación Básica. En primer lugar se ofrece una cápsula informativa acerca de la teoría que sustenta la enseñanza del contenido de exponentes.

A continuación, se presenta un ítem clonado de la prueba de matemáticas que resuelven los estudiantes de tercero básico en las evaluaciones nacionales que aplica la DIGEDUCA, con la finalidad que el docente ubique dentro de lo que establece el Curriculum Nacional Base –CNB–, la destreza evaluada y el contenido por medio del cual se persigue desarrollar la competencia propuesta.

En el apartado Análisis del error, se explican las posibles causas que llevaron a los estudiantes a seleccionar una opción incorrecta. Aquí radica la razón del título de esta publicación. Se espera que los docentes utilicen este análisis para identificar las posibles deficiencias y promover estrategias para fortalecer los aprendizajes. Como complemento del análisis del error, se brindan algunas sugerencias para mejorar los aprendizajes, que desde luego no quedan agotadas en este bifoliar.

Finalmente se refiere una lista de referencias bibliográficas que pueden ser consultadas para completar la información aquí incluida. La DIGEDUCA espera con esta publicación, hacer un aporte que favorezca la calidad educativa de la enseñanza en nuestro país.

Exponentes

Si n es un entero positivo, la notación exponencial aⁿ representa el producto del número real a multiplicado n veces por sí mismo y se define de la forma: aⁿ = a∙a∙a∙a∙a…a. Las leyes de los exponentes son reglas que permiten simplificar expresiones. Si a y b son números reales cualesquiera, entonces:

Simplificar una expresión que posee potencias significa cambiarla a otra equivalente aplicando las leyes de los exponentes de tal forma que cada número real aparece solo una vez y todos los exponentes son positivos, por ejemplo para simplificar la expresión:( 3x³y⁶) ∙ (4xy²) se utiliza la ley de los exponentes a^m ∙ aⁿ = a^m+n de la siguiente forma: Los factores se acomodan:(3)(4)x³xy⁶y², se aplica la ley (1) para simplificar a: 12 x⁴ y⁸

Análisis del ítem

Al incluir ítems de exponentes se espera que el estudiante evidencie que utiliza correctamente la simplificación de expresiones.

Al simplificar la expresión el resultado que se obtiene es: a. 4x9 b. 12x6 c. 4 x6 d. 2 x5

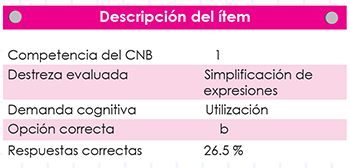
La demanda cognitiva de este ítem, ubicada en Utilización, requiere del estudiante recordar las leyes de los exponentes, elegir la que corresponde y aplicarla correctamente para luego simplificar la expresión.

Análisis del error

Previo a la enseñanza de las leyes de los exponentes refuerce los conocimientos básicos de los estudiantes en: Las propiedades de los números reales Las operaciones básicas de los números reales Potenciación

El ítem consiste en una expresión que contiene dos exponentes; el primero se aplica solo a la variable x, el segundo se aplica a la expresión (6x3). Los estudiantes deben simplificar la expresión respetando el orden en la jerarquía de operaciones: y seleccionar la opción que muestra esta respuesta.

Los posibles errores cometidos por los estudiantes son los siguientes: Si el estudiante eligió la opción…

a. No respeta el orden en la jerarquía de operaciones al resolver el cociente 6/3 directamente y obtiene la expresión ( 2x³)², que no es equivalente a la expresión original, para resolver esta expresión establece que (2²)(x³)2 es 4x⁹, la respuesta indica que no aplica correctamente la ley de los exponentes al escribir que 3² es 9.

c. No comprende la potenciación y resuelve que el numerador de la expresión ( 6x³)² es 12x⁶, este resultado lo obtiene de multiplicar 6∙2 y obtener 12 y el exponente de x como el producto de 3∙2. El resultado del numerador lo divide entre 3 y obtiene 4x⁶

d. Emplea de forma incorrecta las leyes de los exponentes al resolver que (x³)² es x³⁺² = x⁵. No comprende que el número 6 es afectado por el exponente 2 y expresa el numerador como: 6x⁵, este resultado lo divide entre 3 y obtiene 2x⁵.

En conclusión, los errores evidencian que los estudiantes no conocen o recuerdan las leyes de exponentes o no eligen adecuadamente cuándo aplicarlas por lo que fallan al simplificar expresiones.

En el CNB la competencia 1 “Produce patrones aritméticos, algebraicos y geométricos, aplicando propiedades y relaciones.”. Para ello, se propone como indicador de logro la aplicación de “factorización de polinomios al simplificar fracciones algebraicas y dividir polinomios.”. Los contenidos declarativos que permitirán desarrollar la competencia prevista son los Polinomios y sus operaciones y propiedades, Productos Notables, Binomio de Newton, Triángulo de Pascal o de Tartaglia y Factorización.

Sugerencias de estrategias de aprendizaje

1. Elabore una hoja de 8 ejercicios como mínimo con nivel de dificultad gradual con las soluciones respectivas, de modo que en cada solución se cometa alguno de los errores comunes que cometen los estudiantes al aplicar las leyes del los exponentes. Asigne al estudiante como tarea que identifique el error cometido y que explique cómo lo resolvería correctamente.
2. Seleccione ejercicios donde se tenga que simplificar expresiones aplicando varias leyes de exponentes. Elabore una hoja con 5 ejercicios como mínimo escribiendo la solución correcta (recuerde que algunas veces hay varias formas de simplificar las expresiones). Asigne a los estudiantes que escriban en cada paso qué ley de exponentes se utilizó. El ejemplo siguiente le sirve de guía: Explique cada una de las leyes de los exponentes que se emplearon para simplificar la expresión

Referencias

Documentos consultados
Barnett, R. Kearns T. (1997). Matemáticas Nivel 4. Segunda Edición. McGraw-Hill. Colombia. Capitulo 2. Pag. 32-110. Swokowsky, E.W y Cole, J.A. (1998). Algebra y Trigonometría. 9ed. International Thomson Editores. México. Pag.15 - 26 Murillo Jesús, I. Definiciones básicas: exponentes y radicales. Álgebra Nivel Medio Superior. Documento recuperado el 8 de junio de 2012. Disponible en: http://azul2.bnct.ipn.mx/algebra/definiciones%20basicas.PDF

Cada una de las partes o unidades de que se compone una prueba, un test o un cuestionario

Habilidad, facilidad o arte para hacer algo bien hecho.

En el continuo de coaching es el rol de ser muy directo y enseñar, mostrar, guiar, etc.