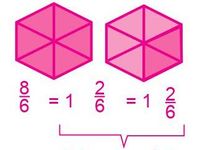Tema 3. Números racionales I
| Línea 92: | Línea 92: | ||
{|class="wikitable" style="width:50%; margin: 10px auto 10px auto;" | {|class="wikitable" style="width:50%; margin: 10px auto 10px auto;" | ||
|- | |- | ||
| − | |style="background:#f067a6; width: | + | |style="background:#f067a6; width:55%; border: 2px solid #ec008d; text-align:center;"|Operación |
| − | |style="background:#f067a6; width: | + | |style="background:#f067a6; width:15%; border: 2px solid #ec008d; text-align:center;"|(a) |
|style="background:#f067a6; width:15%; border: 2px solid #ec008d; text-align:center;"|(b) | |style="background:#f067a6; width:15%; border: 2px solid #ec008d; text-align:center;"|(b) | ||
|style="background:#f067a6; width:15%; border: 2px solid #ec008d; text-align:center;"| (c) | |style="background:#f067a6; width:15%; border: 2px solid #ec008d; text-align:center;"| (c) | ||
|- | |- | ||
| − | |style="background:#fff; width: | + | |style="background:#fff; width:55%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{3}{5}-\frac{6}{5}+\frac{4}{5}+\frac{3}{5}</math>=?</span> |
| − | |style="background:#fff; width: | + | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{4}{10}</math></span> |
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{10}{5}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{10}{5}</math></span> | ||
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{4}{5}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{4}{5}</math></span> | ||
|- | |- | ||
| − | |style="background:#fff; width: | + | |style="background:#fff; width:55%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{x}{3}-\frac{2x}{3}+\frac{5x}{3}</math>=?</span> |
| − | |style="background:#fff; width: | + | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{4x}{3}</math></span> |
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{6x}{3}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{6x}{3}</math></span> | ||
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{2x}{6}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{2x}{6}</math></span> | ||
|- | |- | ||
| − | |style="background:#fff; width: | + | |style="background:#fff; width:55%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{2}{3}+\frac{1}{6}+\frac{7}{12}</math>=?</span> |
| − | |style="background:#fff; width: | + | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{10}{21}</math></span> |
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{15}{12}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{15}{12}</math></span> | ||
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{10}{3}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{10}{3}</math></span> | ||
|- | |- | ||
| − | |style="background:#fff; width: | + | |style="background:#fff; width:55%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{15}{y}-\frac{10}{y}-\frac{17}{6}</math>=?</span> |
| − | |style="background:#fff; width: | + | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{8}{3y}</math></span> |
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{8}{y}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{8}{y}</math></span> | ||
|style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{8}{y^3}</math></span> | |style="background:#fff; width:15%; border: 2px solid #ec008d;"|<span style="font-size:20px"><math>\frac{8}{y^3}</math></span> | ||
Revisión del 02:12 3 jul 2020
Inicio
Indicadores de logro
- Determina las fracciones equivalentes de una fracción irreducible.
- Expresa fracciones impropias y fracciones mixtas.
- Suma y resta fracciones con denominadores comunes y denominadores diferentes.
Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del Ciclo Básico.
1. Lea y resuelva.
La biblioteca municipal cuenta con 2,950 libros. En una librera están colocados los de historia y poesía que conforman la mitad de libros en existencia. En otra librera se encuentra el resto de los libros distribuidos de la manera siguiente: de ciencias básicas ocupan un cuarto del espacio; de matemática, la mitad de la librera; y las revistas, ocupan el otro cuarto de la librera.
¿Cuántos libros de ciencias básicas y Matemáticas hay en la biblioteca?
- Plantee una estrategia para hallar la cantidad de libros.
- Comparta con los compañeros sus hallazgos.
- Compare sus resultados con otros compañeros.
2. Lea, resuelva y exponga resultados.
Enrique le dice a su amiga Julia que él vive a una distancia aproximada de 13/15 kilómetros a la derecha de Gilberto. Por su parte, Julia le indica a Enrique que ella considera que vive a 7/8 a la izquierda de Gilberto.
- Ubique la información en una recta numérica y establezca quién vive más cerca de Gilberto.
- Proponga otras estrategias que se pueden utilizar para determinar quién vive más cerca.
Fernando, Diana y Elsa tienen que pintar un cuadro para la clase de dibujo. Fernando emplea la mitad del día en hacerlo; Diana, las dos terceras partes del día; y Elsa, una tercera parte. - ¿Quién ha tardado más tiempo en hacer el cuadro? ¿Quién menos?
- Comparta la estrategia que usó para resolver el problema.
- Explique como encontró la respuesta.
- Converse con un compañero acerca de las formas en que aprende sobre estos procesos.
Desarrollo
Nuevos aprendizajes
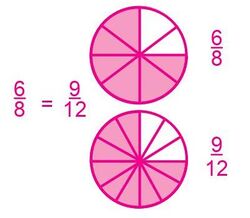
El símbolo [math]\displaystyle{ \frac {a}{b} }[/math] , donde a y b son números cardinales y b ≠ 0, se llama fracción. El número que esta sobre la barra es el numerador; el número que está debajo es el denominador. Una fracción puede describir una región o un conjunto. Las fracciones que representan la misma cantidad se llaman fracciones equivalentes. Si se multiplica o se divide el numerador y denominador por una cantidad diferente de cero obtengo una fracción equivalente.
1. Copie en el cuaderno las operaciones indicadas, para hallar fracciones equivalentes.
Ej. [math]\displaystyle{ \frac{7}{5} }[/math]*[math]\displaystyle{ \frac{6}{6} }[/math] = [math]\displaystyle{ \frac{42}{30} }[/math]
[math]\displaystyle{ \frac{10}{16} }[/math]*[math]\displaystyle{ \frac{3}{3} }[/math] = [math]\displaystyle{ \frac{\Box}{\Box} }[/math]
[math]\displaystyle{ \frac{8}{20} }[/math][math]\displaystyle{ \div \frac{2}{2} }[/math] = [math]\displaystyle{ \frac{\Box}{\Box} }[/math]
[math]\displaystyle{ \frac{4}{4} }[/math]*[math]\displaystyle{ \frac{5}{5} }[/math] = [math]\displaystyle{ \frac{\Box}{\Box} }[/math]
[math]\displaystyle{ \frac{25}{75} }[/math][math]\displaystyle{ \div \frac{25}{25} }[/math] = [math]\displaystyle{ \frac{\Box}{\Box} }[/math]
Fracciones propias e impropias
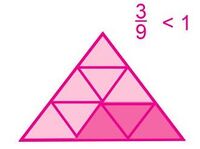
Una fracción propia es cuando el numerador es menor que el denominador. Si su numerador es mayor o igual que su denominador, entonces es una fracción impropia. Cuando una fracción impropia se escribe en forma de un entero y una fracción, se llama numeral mixto o número mixto.
2. Represente en el cuaderno de forma geométrica los números:
- Trace una recta numérica y localice los números anteriores.
- Establezca quién es el mayor y el menor, según su posición en la recta numérica.
- Compare las representaciones con sus compañeros.
2[math]\displaystyle{ \frac{2}{5} }[/math]; [math]\displaystyle{ \frac{4}{5} }[/math]; 1 [math]\displaystyle{ \frac{3}{4} }[/math] y [math]\displaystyle{ \frac{5}{2} }[/math]
Fracciones de igual denominador
Para sumar (adicionar) o restar (sustraer) fracciones de igual denominador se copia el denominador y se suman o restan los numeradores. Si son de diferente denominador, se convierten en fracciones equivalentes para expresarlas con igual denominador.
- Represente geométricamente las operaciones:
[math]\displaystyle{ \frac {5}{7}+\frac {3}{7}-\frac {6}{7}=\frac {2}{7} }[/math]
- Represente de forma geométrica la suma:
3[math]\displaystyle{ \frac {1}{2}+\frac {3}{2}=\frac {10}{2} }[/math]
Cierre
Ejercicios del tema
Nivel: Conocimiento y recuerdo. Identifica y examina las situaciones
1. Conteste (V) verdadero o (F) falso a las siguientes afirmaciones y corrija en el cuaderno aquellas que sean falsas:
- a)[math]\displaystyle{ \frac{29}{6} }[/math] y [math]\displaystyle{ \frac{9}{6} }[/math] son equivalentes ( )
- b)La fracción [math]\displaystyle{ \frac{2}{3} }[/math]es la fracción irreducible de [math]\displaystyle{ \frac{4}{12} }[/math] ( )
- c) Es lo mismo comer [math]\displaystyle{ \frac{4}{5} }[/math]de pastel que [math]\displaystyle{ \frac{20}{25} }[/math] ( )
2. Seleccione entre las opciones la respuesta correcta.
| Operación | (a) | (b) | (c) |
| [math]\displaystyle{ \frac{3}{5}-\frac{6}{5}+\frac{4}{5}+\frac{3}{5} }[/math]=? | [math]\displaystyle{ \frac{4}{10} }[/math] | [math]\displaystyle{ \frac{10}{5} }[/math] | [math]\displaystyle{ \frac{4}{5} }[/math] |
| [math]\displaystyle{ \frac{x}{3}-\frac{2x}{3}+\frac{5x}{3} }[/math]=? | [math]\displaystyle{ \frac{4x}{3} }[/math] | [math]\displaystyle{ \frac{6x}{3} }[/math] | [math]\displaystyle{ \frac{2x}{6} }[/math] |
| [math]\displaystyle{ \frac{2}{3}+\frac{1}{6}+\frac{7}{12} }[/math]=? | [math]\displaystyle{ \frac{10}{21} }[/math] | [math]\displaystyle{ \frac{15}{12} }[/math] | [math]\displaystyle{ \frac{10}{3} }[/math] |
| [math]\displaystyle{ \frac{15}{y}-\frac{10}{y}-\frac{17}{6} }[/math]=? | [math]\displaystyle{ \frac{8}{3y} }[/math] | [math]\displaystyle{ \frac{8}{y} }[/math] | [math]\displaystyle{ \frac{8}{y^3} }[/math] |
| 3) De los números al álgebra | ||
| Evalúe cada expresión y escriba en forma de número mixto. Observe el ejemplo. | ||
| 0) | [math]\displaystyle{ \frac {a}{b} }[/math] para a = 23; b =5 | [math]\displaystyle{ \frac {23}{5} }[/math]=4 [math]\displaystyle{ \frac {3}{4} }[/math] |
| 1) | [math]\displaystyle{ \frac {m}{n} }[/math]para m = 73; =17 | |
| 2) | [math]\displaystyle{ \frac {2w}{z} }[/math] para w = 33; z =5 | |
| 3) | [math]\displaystyle{ \frac {u}{2v} }[/math] para u = 27; v =11 | |
Nivel: Comprensión. Lea y resuelva las siguientes situaciones
3. Exponga con un cartel.
Se organizó un maratón de 5 km. ¿Cuál es el orden en que podemos ubicar carteles a lo largo del camino que indiquen recorridos de: [math]\displaystyle{ \frac {1}{2} }[/math] km; [math]\displaystyle{ \frac {17}{5} }[/math]km; [math]\displaystyle{ \frac {13}{3} }[/math]km?
4. Trace una recta numérica y ubique las marcas, comparta los resultados.
Los albañiles han pintado [math]\displaystyle{ \frac {5}{8} }[/math] de una pared de color azul, [math]\displaystyle{ \frac {1}{4} }[/math] de gris y el resto no está pintada todavía.
- ¿Qué porción de la pared está pintada? ¿Qué parte no está pintada?
- Calcule y comparta la estrategia que usó.
5. Si un lado de una ventana de forma cuadrada es de [math]\displaystyle{ \frac {6b}{8} }[/math]
- Dibuje el cuadrado e identifique sus lados, luego sumando sus lados para saber su perímetro.
- Calcule el perímetro de la ventana si el lado es: b=2 4/12
Nivel: Análisis. Ordena los datos y plantea estrategias
6. Observe y copie en el cuaderno el ejemplo y solucione los ejercicios que se muestran en la Tabla 1.
Estuardo se fue de viaje y durante la primera hora realizó [math]\displaystyle{ \frac {1}{3} }[/math] de camino y en la hora siguiente recorrió [math]\displaystyle{ \frac {2}{5} }[/math] del camino.
- ¿Qué parte del camino recorrió Estuardo en esas horas?
- ¿Qué parte del viaje falta?
- Trace una recta numérica para ubicar los recorridos
- Comparta sus resultados y explique.
De una bolsa de caramelos, Oscar sacó [math]\displaystyle{ \frac {1}{4} }[/math] y María [math]\displaystyle{ \frac {1}{3} }[/math]
- ¿Qué parte de los caramelos quedó en la bolsa?
- Represente geométricamente la situación.
- Comparta sus resultados.
| De los números al álgebra | |
| Números | Álgebra |
| [math]\displaystyle{ \frac{6}{15}=\frac{2*\lt del\gt 3\lt /del\gt }{5*\lt del\gt 3\lt /del\gt }=\frac{2}{5} }[/math] | |