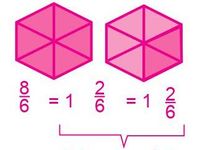Tema 3. Números racionales I

Inicio

Indicadores de logro

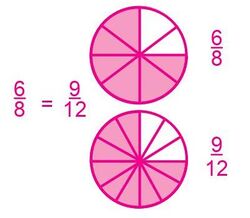
1. Determina las fracciones equivalentes de una fracción irreducible.
2. Expresa fracciones impropias y fracciones mixtas.
3. Suma y resta fracciones con denominadores comunes y denominadores diferentes.

Todas las actividades de este tema son para que usted realice. Si tiene oportunidad reúnase con otros docentes y compartan. Se recomienda aplicarlas con sus estudiantes del Ciclo Básico.

1. Lea y resuelva.

La biblioteca municipal cuenta con 2,950 libros. En una librera están colocados los de historia y poesía que conforman la mitad de libros en existencia. En otra librera se encuentra el resto de los libros distribuidos de la manera siguiente: de ciencias básicas ocupan un cuarto del espacio; de matemática, la mitad de la librera; y las revistas, ocupan el otro cuarto de la librera.

¿Cuántos libros de ciencias básicas y Matemáticas hay en la biblioteca?

• Plantee una estrategia para hallar la cantidad de libros.
• Comparta con los compañeros sus hallazgos.
• Compare sus resultados con otros compañeros.

2. Lea, resuelva y exponga resultados.

Enrique le dice a su amiga Julia que él vive a una distancia aproximada de 13/15 kilómetros a la derecha de Gilberto. Por su parte, Julia le indica a Enrique que ella considera que vive a 7/8 a la izquierda de Gilberto.

• Ubique la información en una recta numérica y establezca quién vive más cerca de Gilberto.
• Proponga otras estrategias que se pueden utilizar para determinar quién vive más cerca.
  Fernando, Diana y Elsa tienen que pintar un cuadro para la clase de dibujo. Fernando emplea la mitad del día en hacerlo; Diana, las dos terceras partes del día; y Elsa, una tercera parte.
• ¿Quién ha tardado más tiempo en hacer el cuadro? ¿Quién menos?
• Comparta la estrategia que usó para resolver el problema.
• Explique como encontró la respuesta.
• Converse con un compañero acerca de las formas en que aprende sobre estos procesos.

Desarrollo

Nuevos aprendizajes

El símbolo $\frac{a}{b}$ , donde a y b son números cardinales y b ≠ 0, se llama fracción. El número que esta sobre la barra es el numerador; el número que está debajo es el denominador. Una fracción puede describir una región o un conjunto. Las fracciones que representan la misma cantidad se llaman fracciones equivalentes. Si se multiplica o se divide el numerador y denominador por una cantidad diferente de cero obtengo una fracción equivalente.

Fracciones equivalentes

1. Copie en el cuaderno las operaciones indicadas, para hallar fracciones equivalentes.

Ej. $\frac{7}{5}$*$\frac{6}{6}$ = $\frac{42}{30}$

$\frac{10}{16}$*$\frac{3}{3}$ = $\frac{◻}{◻}$

$\frac{8}{20}$$÷\frac{2}{2}$ = $\frac{◻}{◻}$

$\frac{4}{4}$*$\frac{5}{5}$ = $\frac{◻}{◻}$

$\frac{25}{75}$$÷\frac{25}{25}$ = $\frac{◻}{◻}$

Fracciones propias e impropias

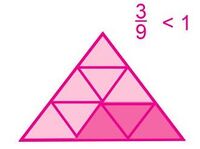
Una fracción propia es cuando el numerador es menor que el denominador. Si su numerador es mayor o igual que su denominador, entonces es una fracción impropia. Cuando una fracción impropia se escribe en forma de un entero y una fracción, se llama numeral mixto o número mixto.

• 

  Fracción propia

• 

  Fracción impropia

2. Represente en el cuaderno de forma geométrica los números:

• Trace una recta numérica y localice los números anteriores.
• Establezca quién es el mayor y el menor, según su posición en la recta numérica.
• Compare las representaciones con sus compañeros.

$2\frac{2}{5}$; $\frac{4}{5}$; $1\frac{3}{4}$ y $\frac{5}{2}$

Fracciones de igual denominador

Para sumar (adicionar) o restar (sustraer) fracciones de igual denominador se copia el denominador y se suman o restan los numeradores. Si son de diferente denominador, se convierten en fracciones equivalentes para expresarlas con igual denominador.

• Represente geométricamente las operaciones:

$\frac{5}{7}+\frac{3}{7}-\frac{6}{7}=\frac{2}{7}$

• Represente de forma geométrica la suma:

$3\frac{1}{2}+\frac{3}{2}=\frac{10}{2}$

Cierre

Ejercicios del tema

Nivel: Conocimiento y recuerdo. Identifica y examina las situaciones

1. Conteste (V) verdadero o (F) falso a las siguientes afirmaciones y corrija en el cuaderno aquellas que sean falsas:

a)$\frac{29}{6}\frac{9}{6}$son equivalentes	( )
b)La fracción $\frac{2}{3}$ es la fracción irreducible de $\frac{4}{12}$	( )
c) Es lo mismo comer $\frac{4}{5}$de pastel que $\frac{20}{25}$	( )

2. Seleccione entre las opciones la respuesta correcta.

Operación	(a)	(b)	(c)
$\frac{3}{5}-\frac{6}{5}+\frac{4}{5}+\frac{3}{5}$=?	$\frac{4}{10}$	$\frac{10}{5}$	$\frac{4}{5}$
$\frac{x}{3}-\frac{2x}{3}+\frac{5x}{3}$=?	$\frac{4x}{3}$	$\frac{6x}{3}$	$\frac{2x}{6}$
$\frac{2}{3}+\frac{1}{6}+\frac{7}{12}$=?	$\frac{10}{21}$	$\frac{15}{12}$	$\frac{10}{3}$
$\frac{15}{y}-\frac{10}{y}-\frac{17}{6}$=?	$\frac{8}{3y}$	$\frac{8}{y}$	$\frac{8}{y^3}$

3) De los números al álgebra
Evalúe cada expresión y escriba en forma de número mixto. Observe el ejemplo.
$0)$	$\frac{a}{b}$ para $a=23;b=5$	$\frac{23}{5}=$ $4\frac{3}{4}$
$1)$	$\frac{m}{n}$ para $m=73;=17$
$2)$	$\frac{2w}{z}$ para $w=33;z=5$
$3)$	$\frac{u}{2v}$ para $u=27;v=11$

Nivel: Comprensión. Lea y resuelva las siguientes situaciones

3. Exponga con un cartel.

Se organizó un maratón de 5 km. ¿Cuál es el orden en que podemos ubicar carteles a lo largo del camino que indiquen recorridos de: $\frac{1}{2}$ km; $\frac{17}{5}$ km; $\frac{13}{3}$ km?

4. Trace una recta numérica y ubique las marcas, comparta los resultados.

Los albañiles han pintado $\frac{5}{8}$ de una pared de color azul, $\frac{1}{4}$ de gris y el resto no está pintada todavía.

• ¿Qué porción de la pared está pintada? ¿Qué parte no está pintada?
• Calcule y comparta la estrategia que usó.

5. Si un lado de una ventana de forma cuadrada es de $\frac{6b}{8}$

• Dibuje el cuadrado e identifique sus lados, luego sumando sus lados para saber su perímetro.
• Calcule el perímetro de la ventana si el lado es: b=2 4/12

Nivel: Análisis. Ordena los datos y plantea estrategias

6. Observe y copie en el cuaderno el ejemplo y solucione los ejercicios que se muestran en la Tabla 1.

Estuardo se fue de viaje y durante la primera hora realizó $\frac{1}{3}$ de camino y en la hora siguiente recorrió $\frac{2}{5}$ del camino.

• ¿Qué parte del camino recorrió Estuardo en esas horas?
• ¿Qué parte del viaje falta?
• Trace una recta numérica para ubicar los recorridos
• Comparta sus resultados y explique.

De una bolsa de caramelos, Oscar sacó $\frac{1}{4}$ y María $\frac{1}{3}$

• ¿Qué parte de los caramelos quedó en la bolsa?
• Represente geométricamente la situación.
• Comparta sus resultados.

Figura 1

De los números al álgebra
Números	Álgebra
$\frac{6}{15}=\frac{2\ast \text{⧸}3}{5\ast \text{⧸}3}=\frac{2}{5}$	$\frac{3am}{5bm}=\frac{3\ast a\ast \text{⧸}m}{5\ast b\ast \text{⧸}m}=\frac{3a}{5b}$
$\frac{15}{21}\frac{◻\ast ◻}{◻\ast ◻}=\frac{◻}{◻}$	$\frac{3x}{15xy}\frac{◻\ast ◻}{◻\ast ◻\ast ◻}=\frac{◻}{◻}$
$\frac{35}{70}$	$\frac{20wy}{45w}$

Nivel: Utilización. Utiliza la información para resolver los planteamientos

7. Resuelva en el cuaderno las siguientes situaciones expresadas como:$\frac{t}{5}+\frac{t}{5}=10$ y $\frac{t}{5}+\frac{t}{5}+10$

• Escriba las diferencias entre ambas situaciones.
• Explique a sus compañeros cómo solucionó cada caso.
• Compare sus estrategias y soluciones.

x es la cantidad de combustible que le queda en el tanque a una camioneta para terminar su recorrido, la expresión $1+\frac{3}{x}=9$ representa la cantidad de combustibles.

• Plantee una estrategia para hallar el valor de x.
• Determine qué fracción de combustible queda y comparta su hallazgo.

8. Establezca una estrategia para resolver el problema y preséntelo en forma gráfica.

• ¡Cómo! ¿Ya no hay leche? –preguntó la madre. –Si ayer compré suficiente para el desayuno.
• La mitad la usó la abuela para el arroz con leche –dijo Alberto.
• Bueno, yo usé la mitad de la que quedó para los licuados esta mañana – dijo Martha.
• Acuérdate que al medio día ocupaste la mitad de la que había para el café –dijo Javier.
• Yo me tomé la mitad de la que quedaba, mientras veía la televisión –agregó Juanito.
• ¿Y solo queda ¼ de litro? –Preguntó el padre–, pero, ¿cuánto compraste ayer?

Resultados a los ejercicios del tema

Compruebe sus resultados a los ejercicios del tema con esta tabla.

Respuestas de la fase de inicio

1. Explique que al sumar se obtiene:$\frac{1}{4}+\frac{1}{2}=\frac{3}{4}$ Al multiplicar$\frac{3}{4}$*1475$\cong$1106 libros

2. Dibuje una recta numérica para ubicar las fracciones luego plantee e identifique Julia: 7/-8=105/120;

Enrique 13/15=104/120, Enrique está más cerca.

Amplifique a denominador 6 para comparar distancias:

Fernando $\frac{1}{2}\to \frac{3}{6}$

Diana $\frac{2}{3}\to \frac{4}{6}$

Elsa $\frac{1}{3}\to \frac{2}{5}$

Más=Diana; Menos=Elsa

Respuestas de la fase de cierre

Ejercicios del tema

Conocimiento y recuerdo: Identifica y examina las situaciones

En esta parte se refuerza la habilidad de poder recordar determinada palabra o concepto, operación y luego emplearlo.

1. a) $26/24=13/12\ne 9/6$, no son equivalentes, b) $2/3;4/12=1/3\ne 2/3$ no son equivalente c) $4/5;20/25=4/5$ son equivalentes.

2. 1) $4/10;$ 2) $4x/3;$ 3) $17/12;$ 4) $8/y$

3. 1)$4\frac{5}{17}$ 2) $6\frac{3}{5}$; $2\frac{5}{11}$

Comprensión: Organiza y relaciona la información

Refuerza lo que lee y, asocia un número, una variable y una operación. La selección de elementos significativos le permite dar respuesta a la situación problemática

Respuestas:

4. Trace una recta numérica y ubique:

$\frac{1}{2};3\frac{2}{5};4\frac{1}{3}$

Calcule la parte pintada: $5/8+1/4=7/8$; parte no pintada: $1-7/8=1/9$

Sume los lados para hallar el perímetro:

$\frac{6b}{8}+\frac{6b}{8}\frac{6b}{8}+\frac{6b}{8}=\frac{24b}{8}=3b$

5. Sustituya para el perímetro = $3\frac{28}{12}=7$

Respuestas de la fase de análisis

Ordena los datos y plantea estrategias

Identifique diferencias y similitudes importantes en el conocimiento.

6. Factorice y simplifique: $\frac{15}{21}=\frac{\text{⧸}3\ast 5}{\text{⧸}3\ast 7}=\frac{5}{7};\frac{3x}{15xy}=\frac{\text{⧸}3\ast x}{\text{⧸}3\ast 5\ast x\ast y}=\frac{1}{5}$

$\frac{35}{70}=\frac{\text{⧸}7\ast \text{⧸}5}{\text{⧸}7\ast \text{⧸}5\ast 2}=\frac{1}{2};\frac{20wy}{45w}=\frac{4\ast \text{⧸}5\ast \text{⧸}wy}{9\ast \text{⧸}5\ast \text{⧸}w}=\frac{4y}{9}$

Calcule $\frac{2}{5}+\frac{1}{3}=\frac{11}{15};$ falta por recorrer $1-\frac{11}{15}=\frac{4}{15};$

Calcule $\frac{1}{4}+\frac{1}{3}=\frac{7}{12};$

caramelos que quedan en la bolsa $1-\frac{7}{12}=\frac{5}{12};$

Utilización. Plantea una estrategia utilizando la información para resolver los problemas

Llegar a soluciones efectivas en este nivel indica que se ha logrado un estímulo que le permite actuar con dominio del conocimiento.

7. Despeje: $t:\frac{2t}{5}\to 2t=50\to t=\frac{50}{2}=25$

la variable tiene un valor determinado.

Sume las fracciones:

$\frac{t+t+50}{5}\to 2t=50\to \frac{2t}{5}+10;$ el resultado es una expresión llamada binomio.

8.Despeje

$x\frac{3}{x}=9+1\to \frac{3}{x}=8\to \frac{3}{8}=x;$

Calcule lo bebido: $\frac{1}{2}+\frac{1}{4}\frac{1}{8}\frac{1}{16}=\frac{15}{16}$

Por lo tanto, lo que sobra es $\frac{1}{16}$ de lo que se compró y esto equivale a un 1/4 de litro por los tanto $\frac{1}{4}÷\frac{1}{16}=4$ litros se compraron.

Capacidad o destreza para hacer algo bien o con facilidad.

Lo que estimula o incita a hacer algo.